题目内容
15.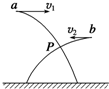 如图所示,a、b两个小球从不同高度同时沿相反方向水平抛出,忽略空气阻力,其平抛运动轨迹的交点为P,则以下说法正确的是( )
如图所示,a、b两个小球从不同高度同时沿相反方向水平抛出,忽略空气阻力,其平抛运动轨迹的交点为P,则以下说法正确的是( )| A. | a、b两球同时落地 | |
| B. | b球先落地 | |
| C. | a、b两球在P点相遇 | |
| D. | 只要两球初速度大小合适,两球就能相遇 |
分析 平抛运动的时间由高度决定,根据高度判断谁先落地,根据到交点P的高度比较运动的时间,从而确定谁先抛出.
解答 解:A、a离地的高度大于b离地的高度,根据t=$\sqrt{\frac{2h}{g}}$知,b球运动的时间短,则b球先落地,故A错误,B正确.
C、运动到P点,a下落的高度较大,可知a球运动的时间较长,可知同时抛出,不可能在P点相遇,故C、D错误.
故选:B.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,知道运动的时间由高度决定,与初速度无关.

练习册系列答案
相关题目
20.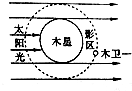 木卫一是最靠近木星的卫星,丹麦天文学家罗迈早在十七世纪通过对木卫一的观测测出了光速.他测量了木卫一绕木星的运动周期T和通过木星影区的时间t.若已知木星的半径R和万有引力恒量G,T远小于木星绕太阳的运行周期,根据以上条件可以求出( )
木卫一是最靠近木星的卫星,丹麦天文学家罗迈早在十七世纪通过对木卫一的观测测出了光速.他测量了木卫一绕木星的运动周期T和通过木星影区的时间t.若已知木星的半径R和万有引力恒量G,T远小于木星绕太阳的运行周期,根据以上条件可以求出( )
 木卫一是最靠近木星的卫星,丹麦天文学家罗迈早在十七世纪通过对木卫一的观测测出了光速.他测量了木卫一绕木星的运动周期T和通过木星影区的时间t.若已知木星的半径R和万有引力恒量G,T远小于木星绕太阳的运行周期,根据以上条件可以求出( )
木卫一是最靠近木星的卫星,丹麦天文学家罗迈早在十七世纪通过对木卫一的观测测出了光速.他测量了木卫一绕木星的运动周期T和通过木星影区的时间t.若已知木星的半径R和万有引力恒量G,T远小于木星绕太阳的运行周期,根据以上条件可以求出( )| A. | 木星的密度 | |
| B. | 木卫一的密度 | |
| C. | 木卫一绕木星运动的向心加速度大小 | |
| D. | 木卫一表面的重力加速度大小 |
4.斜向上方抛出一物体,运动到最高点时,速度( )
| A. | 为零 | B. | 达到最大值 | C. | 一定不为零 | D. | 无法确定 |
5.人造卫星绕地球做匀速圆周运动,其轨道半径为R,线速度为v,周期为T,若使该卫星的周期变为2T,可行的办法是( )
| A. | R不变,线速度变为$\frac{v}{2}$ | B. | v不变,使轨道半径变为2R | ||
| C. | 轨道半径变为$\root{3}{4}$R | D. | v不变,使轨道半径变为$\frac{R}{2}$ |
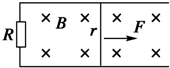 如图所示,直导线可在平行导轨上接触良好且无摩擦地滑动,导轨电阻不计.导轨一端接有定值电阻R=10Ω,直导线的电阻r=2Ω,有效长度L=0.4m,磁感强度B=0.6T的匀强磁场方向与导轨所在平面垂直.当直导线以v=10m/s的速度向右匀速滑动时,求:
如图所示,直导线可在平行导轨上接触良好且无摩擦地滑动,导轨电阻不计.导轨一端接有定值电阻R=10Ω,直导线的电阻r=2Ω,有效长度L=0.4m,磁感强度B=0.6T的匀强磁场方向与导轨所在平面垂直.当直导线以v=10m/s的速度向右匀速滑动时,求: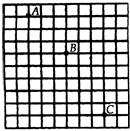 如图所示,用数码相机记录物体做平抛运动的部分轨迹,背景方格的边长为5cm,重力加速度g=10m/s2.该数码相机每次拍摄的时间间隔为0.1s.物体运动中水平速度的大小为1.5m/s.
如图所示,用数码相机记录物体做平抛运动的部分轨迹,背景方格的边长为5cm,重力加速度g=10m/s2.该数码相机每次拍摄的时间间隔为0.1s.物体运动中水平速度的大小为1.5m/s.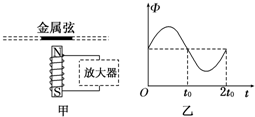
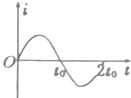
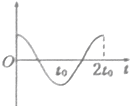
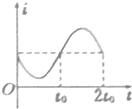
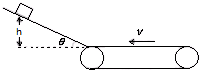 如图所示为一传送带装置模型,斜面的倾角θ,底端经一长度可忽略的光滑圆弧与足够长的水平传送带相连接,质量m=2kg 的物体从高h=30cm的斜面上由静止开始下滑,它与斜面的动摩擦因数μ1=0.25,与水平传送带的动摩擦因数μ2=0.5,物体在传送带上运动一段时间以后,物体又回到了斜面上,如此反复多次后最终停在斜面底端.已知传送带的速度恒为v=2.5m/s,tanθ=0.75,g取10m/s2.求:
如图所示为一传送带装置模型,斜面的倾角θ,底端经一长度可忽略的光滑圆弧与足够长的水平传送带相连接,质量m=2kg 的物体从高h=30cm的斜面上由静止开始下滑,它与斜面的动摩擦因数μ1=0.25,与水平传送带的动摩擦因数μ2=0.5,物体在传送带上运动一段时间以后,物体又回到了斜面上,如此反复多次后最终停在斜面底端.已知传送带的速度恒为v=2.5m/s,tanθ=0.75,g取10m/s2.求: 如图是研究小球的平抛运动时拍摄的闪光照片的一部分,其背景是边长为5厘米的小方格,重力加速度取g=10m/.由此可知:闪光频率为10Hz;小球抛出时的初速度大小为2.5m/s;从抛出A到C点,小球速度的改变量为2m/s.
如图是研究小球的平抛运动时拍摄的闪光照片的一部分,其背景是边长为5厘米的小方格,重力加速度取g=10m/.由此可知:闪光频率为10Hz;小球抛出时的初速度大小为2.5m/s;从抛出A到C点,小球速度的改变量为2m/s.