题目内容
5.人造卫星绕地球做匀速圆周运动,其轨道半径为R,线速度为v,周期为T,若使该卫星的周期变为2T,可行的办法是( )| A. | R不变,线速度变为$\frac{v}{2}$ | B. | v不变,使轨道半径变为2R | ||
| C. | 轨道半径变为$\root{3}{4}$R | D. | v不变,使轨道半径变为$\frac{R}{2}$ |
分析 人造地球卫星绕地球做匀速圆周运动,由地球的万有引力提供向心力,牛顿第二定律推导周期T与半径的关系,选择可能的办法.若半径R不变,使卫星的线速度减小,卫星将做近心运动,周期减小.若v不变,卫星只能在原轨道上运动,周期不变
解答 解:A、若半径R不变,使卫星的线速度减小,卫星将做近心运动,周期减小.故A错误.
B、若v不变,卫星只能在原轨道上运动,半径不变,周期也不变.故BD错误.
C、设地球的质量为M,卫星的质量为m.由牛顿第二定律得:$G\frac{Mm}{{R}^{2}}=m\frac{4{π}^{2}R}{{T}^{2}}$
得到T=$2π\sqrt{\frac{{R}^{3}}{GM}}$
根据数学知识可知,使轨道半径R变为$\root{3}{4}R$时,卫星的周期变2T.故C正确;
故选:C
点评 本题考查卫星的变轨问题,当卫星的速度增加时,做离心运动,半径增加;当卫星速度减小,做近心运动,半径减小.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
15.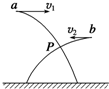 如图所示,a、b两个小球从不同高度同时沿相反方向水平抛出,忽略空气阻力,其平抛运动轨迹的交点为P,则以下说法正确的是( )
如图所示,a、b两个小球从不同高度同时沿相反方向水平抛出,忽略空气阻力,其平抛运动轨迹的交点为P,则以下说法正确的是( )
 如图所示,a、b两个小球从不同高度同时沿相反方向水平抛出,忽略空气阻力,其平抛运动轨迹的交点为P,则以下说法正确的是( )
如图所示,a、b两个小球从不同高度同时沿相反方向水平抛出,忽略空气阻力,其平抛运动轨迹的交点为P,则以下说法正确的是( )| A. | a、b两球同时落地 | |
| B. | b球先落地 | |
| C. | a、b两球在P点相遇 | |
| D. | 只要两球初速度大小合适,两球就能相遇 |
13.物体做曲线运动时( )
| A. | 速度的方向时刻在改变 | B. | 速度的大小一定会改变 | ||
| C. | 速度的方向不能确定 | D. | 加速度的大小一定会改变 |
20.对牛顿第三定律的理解,下列说法中正确的是( )
| A. | 先产生作用力,后产生反作用力 | |
| B. | 弹力和摩擦力都有反作用力,而重力没有反作用力 | |
| C. | 作用力是弹力,其反作用力可以是摩擦力 | |
| D. | 作用力和反作用力,这两个力在任何情况下都不会平衡 |
10.对万有引力定律的表达式F=G$\frac{{m}_{1}{m}_{2}}{{r}^{2}}$,下列说法正确的是( )
| A. | 公式中G为常量,没有单位,是人为规定的 | |
| B. | r趋向于零时,万有引力趋近于无穷大 | |
| C. | 两物体之间的万有引力总是大小相等,与m1、m2是否相等无关 | |
| D. | 两个物体间的万有引力总是大小相等,方向相反的,是一对平衡力 |
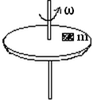
17.如图,小物体m与水平圆盘始终保持相对静止,圆盘绕竖直轴匀速转动,则物体的受力情况是( )

| A. | 受重力、支持力、静摩擦力和向心力的作用 | |
| B. | 摩擦力的方向与小物体速度方向相同 | |
| C. | 小物体所需向心力大小等于其所受摩擦力 | |
| D. | 小物体所需向心力大小大于其所受摩擦力 |
14.关于重力势能与重力做功的下列说法中正确的是( )
| A. | 重力对物体做的功等于重力势能的增加 | |
| B. | 在物体下落的过程中,如果重力做的功相等,物体所减少的重力势能一定相等 | |
| C. | 重力势能等于零的物体,不可能对别的物体做功 | |
| D. | 用手托住物体匀速上举时,手的支特力做的功等于克服重力做的功与物体所增加的重力势能之和 |
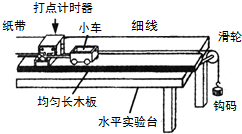 利用图示装置可以做力学中的许多实验.
利用图示装置可以做力学中的许多实验.