Question

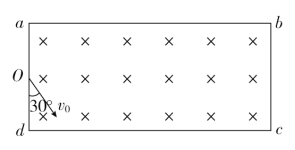
【题目】如图所示，一矩形区域abcd内充满磁感应强度大小为B、方向垂直纸面向里的匀强磁场，现从矩形区域ad边中点O射出与Od边夹角为30°、速度大小为v0的带正电粒子，已知粒子质量为m，电荷量为q，ad边长为L，ab边足够长，粒子重力忽略不计，求：

(1)粒子能从ab边上射出磁场的v0的大小范围；

(2)粒子在磁场中运动的最长时间和在这种情况下粒子从磁场中射出所在边上位置的范围。

Answer 1

【答案】(1) (2)，距O点上方的范围内

【解析】

（1）画出从O点射入磁场的粒子运动轨迹的动态圆，能够从ab边射出的粒子的临界轨迹如图所示，轨迹与dc边相切时，射到ab边上的A点，此时轨迹圆心为O1，则

r1－r1sin30°＝

轨迹半径

r1＝L

即O1点在ab上。

由

得最大速度

。

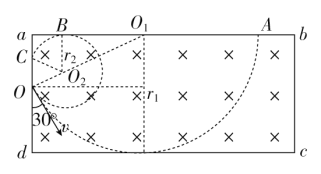
轨迹与ab边相切时，恰不能从ab边射出，切点为ab边上的B点，此时轨迹圆心为O2，则

r2＋r2sin30°＝

轨道半径

r2＝，

由得

所以粒子能够从ab边射出的速度范围为：

（2）由可知，所有粒子的运动周期相同，当运动轨迹所对的圆心角最大时，运动时间最长。当粒子从ad边射出时，时间均相等，且为最长时间，因转过的圆心角为300°，所以最长时间：

。

当运动轨迹恰与ab边相切时，恰能从ad边射出，设射出点为C，则射出的范围为

OC＝r2＝。