题目内容
14. 如图a,b,把劲度系数分别为k1和k2两轻弹簧连接后,施加作用力F,设其整体形变量为△x,则依胡克定律可写为F=k′△x,这就是说两个如图连接的弹簧,对外作用完全可以用一个劲度系数为k′的弹簧代替,k′称为等效劲度系数,试求k′与k1,k2关系表达式.
如图a,b,把劲度系数分别为k1和k2两轻弹簧连接后,施加作用力F,设其整体形变量为△x,则依胡克定律可写为F=k′△x,这就是说两个如图连接的弹簧,对外作用完全可以用一个劲度系数为k′的弹簧代替,k′称为等效劲度系数,试求k′与k1,k2关系表达式.
分析 根据两弹簧的连接方式,利用胡克定律求解合力与形变量之间的关系,即可明确总的劲度系数表达式.
解答 解:如果两个串联:由于弹簧内部弹力处处相等,k1的伸长量为:F=k1x1,k2的伸长量为:F=k2x2;
如果当成一根弹簧,则弹簧的伸长量为:x=x1+x2,而这一根弹簧产生的弹力仍然是F
故有:F=k′x
代入有:F=k′(x2+x1)=k'($\frac{F}{{K}_{1}}$+$\frac{F}{{K}_{2}}$)
消去F,有$\frac{1}{K′}$=$\frac{1}{{k}_{1}}$+$\frac{1}{{k}_{2}}$=$\frac{{k}_{1}{k}_{2}}{{k}_{1}{+k}_{2}}$
如果两个弹簧并联,这两个弹簧产生的弹力之和等于F,
则可F=k′x=kx1+kx2;
即:k'=k1+k2
答:两弹簧串联时,等效劲度系数为:$\frac{{k}_{1}{k}_{2}}{{k}_{1}{+k}_{2}}$;而两弹簧并联时等效劲度系数为k1+k2
点评 本题考查胡克定律的应用,要注意明确胡克定律中x为弹簧的形变量.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
4.关于电场线,下列说法正确的是( )
| A. | 电场线一定是带电粒子在电场中受力的方向 | |
| B. | 电场线不能形象地表示电场强度的方向 | |
| C. | 电场线从正电荷或无限远出发,终止于无限远或负电荷 | |
| D. | 两条电场线在电场中可以相交 |
5. 如图所示,卫星变轨时,要经过一个与小圆和大圆轨道均相切的椭圆轨道,卫星在小圆轨道上的速率为v1,运动到椭圆与小圆的切点P突然加速到速率v2进入椭圆轨道,当卫星沿椭圆轨道运动到与大圆相切的点Q时速率为v3,在Q点再突然加速度到速率v4后沿大圆轨道运动,下列关于四个速率的关系中,正确的是( )
如图所示,卫星变轨时,要经过一个与小圆和大圆轨道均相切的椭圆轨道,卫星在小圆轨道上的速率为v1,运动到椭圆与小圆的切点P突然加速到速率v2进入椭圆轨道,当卫星沿椭圆轨道运动到与大圆相切的点Q时速率为v3,在Q点再突然加速度到速率v4后沿大圆轨道运动,下列关于四个速率的关系中,正确的是( )
 如图所示,卫星变轨时,要经过一个与小圆和大圆轨道均相切的椭圆轨道,卫星在小圆轨道上的速率为v1,运动到椭圆与小圆的切点P突然加速到速率v2进入椭圆轨道,当卫星沿椭圆轨道运动到与大圆相切的点Q时速率为v3,在Q点再突然加速度到速率v4后沿大圆轨道运动,下列关于四个速率的关系中,正确的是( )
如图所示,卫星变轨时,要经过一个与小圆和大圆轨道均相切的椭圆轨道,卫星在小圆轨道上的速率为v1,运动到椭圆与小圆的切点P突然加速到速率v2进入椭圆轨道,当卫星沿椭圆轨道运动到与大圆相切的点Q时速率为v3,在Q点再突然加速度到速率v4后沿大圆轨道运动,下列关于四个速率的关系中,正确的是( )| A. | v2-v3=v1-v4 | B. | v2-v3>v1-v2 | C. | v2-v3<v1-v4 | D. | $\frac{{v}_{2}}{{v}_{3}}=\frac{{v}_{1}}{{v}_{4}}$ |
2.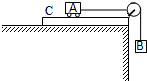 带滑轮的平板C固定在水平桌面上,小车A通过绕过滑轮的轻绳与物体B相连,如图所示,平板C上表面光滑,A的质量为m,物体B的质量为M,设绳中张力为FT.在每次进行改变质量的操作后都由静止释放小车,则对FT相应变化的判断成立的是( )
带滑轮的平板C固定在水平桌面上,小车A通过绕过滑轮的轻绳与物体B相连,如图所示,平板C上表面光滑,A的质量为m,物体B的质量为M,设绳中张力为FT.在每次进行改变质量的操作后都由静止释放小车,则对FT相应变化的判断成立的是( )
 带滑轮的平板C固定在水平桌面上,小车A通过绕过滑轮的轻绳与物体B相连,如图所示,平板C上表面光滑,A的质量为m,物体B的质量为M,设绳中张力为FT.在每次进行改变质量的操作后都由静止释放小车,则对FT相应变化的判断成立的是( )
带滑轮的平板C固定在水平桌面上,小车A通过绕过滑轮的轻绳与物体B相连,如图所示,平板C上表面光滑,A的质量为m,物体B的质量为M,设绳中张力为FT.在每次进行改变质量的操作后都由静止释放小车,则对FT相应变化的判断成立的是( )| A. | 当m不变,M逐次增大时,FT增大,且大小趋向于Mg | |
| B. | 当m不变,M逐次减小时,FT减小,且大小趋向于Mg | |
| C. | 当M不变,m逐次增大时,FT减小,且大小趋向于Mg | |
| D. | 当M不变,m逐次减小时,FT减小,且大小趋向于mg |
19.关于力做的功,下列说法正确的是( )
| A. | 作用力做正功与反作用力肯定做负功 | |
| B. | 作用力做功大小一定等于反作用力做功大小 | |
| C. | 滑动摩擦力可以做正功也可以做负功 | |
| D. | 静摩擦力一定不做功 |
3.下列说法正确的是( )
| A. | 对于受迫振动,驱动力频率越大,受迫振动的振幅一定越大 | |
| B. | 一切波都能发生衍射,衍射是波特有的现象 | |
| C. | 波源与观察者互相靠近或者互相远离时,接收到的频率会发生变化 | |
| D. | 紫外线具有较高的能量,许多物质在紫外线的照射下会发出荧光 | |
| E. | 光速在任何条件下都是3×108m/s |
4. 一个静止的放射性原子核处于垂直纸面向里的匀强磁场中,由于发生了衰变而形成如图所示的两个圆形径迹,两个圆的关径之比为1:16,则( )
一个静止的放射性原子核处于垂直纸面向里的匀强磁场中,由于发生了衰变而形成如图所示的两个圆形径迹,两个圆的关径之比为1:16,则( )
 一个静止的放射性原子核处于垂直纸面向里的匀强磁场中,由于发生了衰变而形成如图所示的两个圆形径迹,两个圆的关径之比为1:16,则( )
一个静止的放射性原子核处于垂直纸面向里的匀强磁场中,由于发生了衰变而形成如图所示的两个圆形径迹,两个圆的关径之比为1:16,则( )| A. | 该原子核发生了α衰变 | |
| B. | 反冲核沿小圆轨道运动且反冲核与粒子运动方向相反 | |
| C. | 原来静止的原子核的原子序数为15 | |
| D. | 沿大圆和沿小圆运动的粒子的周期相等 |
 如图1,风力发电是目前可再生能源中技术比较成熟,具有规模化开发条件和商业发展前景的发电技术.小型独立风力发电系统一般不并网发电,只能独立使用,单台装机容量通常不超过10KW.它的构成为:风力发电机+充电器+数字逆变器.风力发电机由机头、转体、尾翼、叶片组成.叶片用来接受风力并通过机头转为电能;尾翼使叶片始终对着来风的方向从而获得最大的风能;转体能使机头灵活地转动以实现尾翼调整方向的功能;机头的转子是永磁体,定子是绕组切割磁感线产生电能.因风量不稳定,故小型风力发电机输出的是13-25V变化的交流电,须经充电器整流再对蓄电池充电,使风力发电机的产生的电能变能化学能.最后经逆变处理后供给用户使用.某学习小组对一小型风力发电机进行测定风速实验:将一铜棒与风力发电系统的输出端构成回路(注:风力发电机与铜棒直接相连,连接导线末画出)如图2所示.铜棒ab长为0.5m,质量0.2Kg,两端用轻铜线相连.整个装置处在竖直向上的匀强磁场中,磁感应强度B=2T.当有风速4m/s吹向风叶,铜棒与竖直方向成37°角且偏向纸内的位置时,铜棒处于受力平衡状态.
如图1,风力发电是目前可再生能源中技术比较成熟,具有规模化开发条件和商业发展前景的发电技术.小型独立风力发电系统一般不并网发电,只能独立使用,单台装机容量通常不超过10KW.它的构成为:风力发电机+充电器+数字逆变器.风力发电机由机头、转体、尾翼、叶片组成.叶片用来接受风力并通过机头转为电能;尾翼使叶片始终对着来风的方向从而获得最大的风能;转体能使机头灵活地转动以实现尾翼调整方向的功能;机头的转子是永磁体,定子是绕组切割磁感线产生电能.因风量不稳定,故小型风力发电机输出的是13-25V变化的交流电,须经充电器整流再对蓄电池充电,使风力发电机的产生的电能变能化学能.最后经逆变处理后供给用户使用.某学习小组对一小型风力发电机进行测定风速实验:将一铜棒与风力发电系统的输出端构成回路(注:风力发电机与铜棒直接相连,连接导线末画出)如图2所示.铜棒ab长为0.5m,质量0.2Kg,两端用轻铜线相连.整个装置处在竖直向上的匀强磁场中,磁感应强度B=2T.当有风速4m/s吹向风叶,铜棒与竖直方向成37°角且偏向纸内的位置时,铜棒处于受力平衡状态.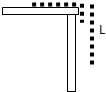 质量为m,长为L的均匀链条,拉直放在光滑水平面上,并让$\frac{L}{3}$吊在桌边外.让链条由静止释放,求:(1)以桌面为0势能点,铁链的机械能是多少?
质量为m,长为L的均匀链条,拉直放在光滑水平面上,并让$\frac{L}{3}$吊在桌边外.让链条由静止释放,求:(1)以桌面为0势能点,铁链的机械能是多少?