题目内容
6.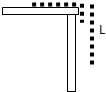 质量为m,长为L的均匀链条,拉直放在光滑水平面上,并让$\frac{L}{3}$吊在桌边外.让链条由静止释放,求:(1)以桌面为0势能点,铁链的机械能是多少?
质量为m,长为L的均匀链条,拉直放在光滑水平面上,并让$\frac{L}{3}$吊在桌边外.让链条由静止释放,求:(1)以桌面为0势能点,铁链的机械能是多少?(2)铁链刚好完全离开桌面时的速度.
分析 (1)设桌面为零势能面,分链条为桌上的部分和桌下的部分分别确定出其两种情况下的重力势能,求出总的机械能.
(2)根据机械能守恒计算最后的速度的大小.
解答 解:(1)选桌面为势能0点,铁链的机械能是
E=$-\frac{1}{3}mg\frac{L}{6}+0$=$-\frac{mgL}{18}$
(2)利用系统机械能守恒,选桌面为势能0点.
初:E=$-\frac{1}{3}mg\frac{L}{6}+0$末:E=$-mg\frac{L}{2}+\frac{1}{2}m{v^2}$
有:$-\frac{1}{3}mg\frac{L}{6}+0=-mg\frac{L}{2}+\frac{1}{2}m{v^2}$,
解得:$v=\frac{2}{3}\sqrt{2gL}$
答:(1)以桌面为0势能点,铁链的机械能是$-\frac{mgL}{18}$;
(2)铁链刚好完全离开桌面时的速度是$\frac{2}{3}\sqrt{2gL}$.
点评 零势能面的选取是任意的,本题也可以选链条滑至刚刚离开桌边时链条的中心为零势能面,结果是一样的,要注意重力势能的正负.

练习册系列答案
相关题目
16.下列陈述中不正确或不符合历史事实的是( )
| A. | 经典力学是以牛顿的三大定律为基础的,它的适应范围是低速、宏观的物体 | |
| B. | 法拉第首先发现电磁感应现象并得出了电磁感应定律 | |
| C. | 牛顿是在伽利略理想斜面实验的基础上进行假想推理得出了牛顿第一定律 | |
| D. | 开普勒通过扭秤实验测出了万有引力常量 |
17. 如图所示的电路,闭合开关S,当滑动变阻器滑片P向右移动时,下列说法正确的是( )
如图所示的电路,闭合开关S,当滑动变阻器滑片P向右移动时,下列说法正确的是( )
 如图所示的电路,闭合开关S,当滑动变阻器滑片P向右移动时,下列说法正确的是( )
如图所示的电路,闭合开关S,当滑动变阻器滑片P向右移动时,下列说法正确的是( )| A. | 电容器C上电荷量减小 | B. | 小灯泡L变暗 | ||
| C. | 电流表读数变小,电压表读数变大 | D. | 电源的总功率变小 |
1.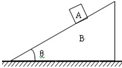 如图所示,物块放在斜面上,随斜面一同在水平方向由左向右匀速运动距离L,物块和斜面始终保持相对静止,关于物块受力做功的情况,下列说法正确的是( )
如图所示,物块放在斜面上,随斜面一同在水平方向由左向右匀速运动距离L,物块和斜面始终保持相对静止,关于物块受力做功的情况,下列说法正确的是( )
 如图所示,物块放在斜面上,随斜面一同在水平方向由左向右匀速运动距离L,物块和斜面始终保持相对静止,关于物块受力做功的情况,下列说法正确的是( )
如图所示,物块放在斜面上,随斜面一同在水平方向由左向右匀速运动距离L,物块和斜面始终保持相对静止,关于物块受力做功的情况,下列说法正确的是( )| A. | 物块受到的支持力做正功 | B. | 物块受到的摩擦力做正功 | ||
| C. | 斜面对物块的作用力做负功 | D. | 斜面对物块的作用力做正功 |
11.放射性元素放出的射线在水平电场中分成A、B、C三束,如图所示,则下列说法正确的是( )


| A. | 电场的方向水平向右 | B. | A高速电子组成的电子流 | ||
| C. | B为比X射线波长更短的光子流 | D. | C为氦核组成的粒子流 |
18.在物理学发展中,许多物理学家的科学发现和学说推动了人类历史进步,下列说法正确的是( )
| A. | 牛顿把地面上物体运动的规律和天体运动的规律统一了起来,建立了万有引力定律 | |
| B. | 伽利略以实验和数学推理相结合的科学研究方法得到了落体运动规律 | |
| C. | 为了解释磁铁和电流都能产生磁场,洛仑兹提出著名的分子电流假说 | |
| D. | 奥斯特发现电流磁效应;法拉第发现了电磁感应现象并制成人类历史上第一台发电机 |
16.下列对于公式E=$\frac{U}{d}$的理解,正确的是( )
| A. | 它仅适用于匀强电场 | |
| B. | 只要测出两点间的电势差和两点间的间距就可以算出电场强度 | |
| C. | 在匀强电场中,场强的数值等于单位距离上降低的电势 | |
| D. | 场强的另一个单位V/m,适用于任何电场 |
 如图a,b,把劲度系数分别为k1和k2两轻弹簧连接后,施加作用力F,设其整体形变量为△x,则依胡克定律可写为F=k′△x,这就是说两个如图连接的弹簧,对外作用完全可以用一个劲度系数为k′的弹簧代替,k′称为等效劲度系数,试求k′与k1,k2关系表达式.
如图a,b,把劲度系数分别为k1和k2两轻弹簧连接后,施加作用力F,设其整体形变量为△x,则依胡克定律可写为F=k′△x,这就是说两个如图连接的弹簧,对外作用完全可以用一个劲度系数为k′的弹簧代替,k′称为等效劲度系数,试求k′与k1,k2关系表达式.
