题目内容
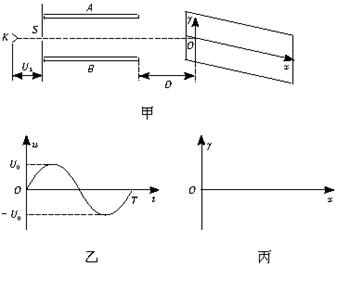
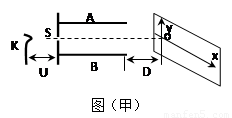
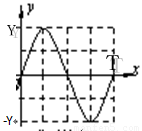
示波器是一种多功能电学仪器,可以在荧光屏显示出被检测的电压波形,它的工作原理如图(一)所示,真空室中电极k发出的电子(初速度为零),经过电压为U1的加速电场后,由小孔S沿水平金属板A、B的中心线射入板中,板长是L,相距为d,在两板间加上如图(二)所示的交流电压,前半个周期内B板的电势高于A板的电势。在每个电子通过极板的极短时间内,电场视为恒定。在两极板右侧且与极板右端相距D处有一个与两板中心线垂直的荧光屏,中心线正好与屏上坐标原点相交。当第一个电子到达坐标原点O时,使屏以速度v沿-x轴方向运动,每经过一定的时间后,在一个极短时间内它又跳回到初始位置,然后重新做同样的匀速运动。求:(1)电子进入AB板时的初速度;(2)要使所有的电子都能打在荧光屏上,图(二)中电压的最大值U0需要满足什么条件?(3)要使荧光屏上始终显示一个完整的波形,荧光屏必须每隔多长时间回到初始位置?计算这个波形的峰值和长度。并在图(三)所示的坐标系中画出这个波形。


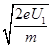
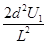
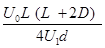 vT
vT
【解析】(1)由动能定理: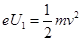 可得
可得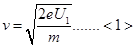
(2)在偏转电场中,偏转电压最大时,侧向位移最大为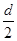 ,则水平方向上
,则水平方向上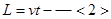
竖直方向上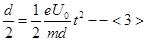
方程<1><2><3>联立解得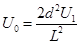
(3) 要使荧光屏上始终显示一个完整的波形,荧光屏运动的周期必须和竖直方向上电压的偏转周期相同,所以每隔T回到初始位置。
在偏转电场中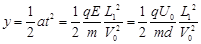 =
=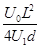
设屏上形成的波形的峰值为Y,根据类平抛的反向延长线过水平位移的中点,所以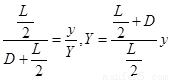 =
=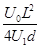
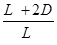 =
=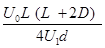 ,
,
波形的长度X=Vt
思路分析:(1)根据动能定理可求飞入偏转电场时的初速度(2)要想都飞出偏转电场,最大侧向位移为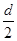 ,根据两个方向上具有等时性,解得最大的U0,(3)利用类平抛的推论,根据相似比求解峰值Y,根据运动的等时性求解波长。
,根据两个方向上具有等时性,解得最大的U0,(3)利用类平抛的推论,根据相似比求解峰值Y,根据运动的等时性求解波长。
试题点评:考查了动能定理、类平抛的分解,类平抛的推论等,是一道计算量很大的综合性难题

 阅读快车系列答案
阅读快车系列答案