题目内容
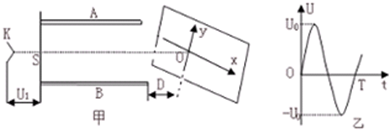
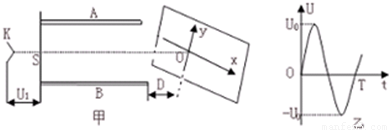
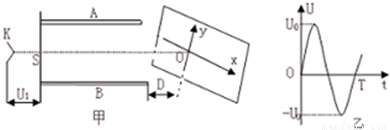
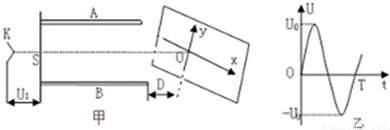
示波器是一种多功能教学仪器,可以在荧光屏上显示出被检测的电压波形.它的工作原理等效成下列情况:如图甲所示,真空室中电极K发出电子(初速不计),经过电压为U1的加速电场后,由小孔S沿水平金属板A.B间的中心线射入板中.板长L,相距为d,在两板间加上如图乙所示的正弦交变电压,前半个周期内B板的电势高于A板的电势,电场全部集中在两板之间,且分布均匀.在每个电子通过极板的极短时间内,电场视作恒定的.在两极板右侧且与极板右侧相距D处有一个与两板中心线垂直的荧光屏,中心线正好与屏上坐标原点相交.当第一个电子到达坐标原点O时,使屏以速度v沿-x方向运动,每经过一定的时间后,在一个极短时间内它又跳回初始位置(可忽略不计),然后重新做同样的匀速运动.已知电子的质量为m,电荷量e,不计电子的重力,求:
(1)电子进入AB板时的初速度.
(2)要使所有的电子都能打在荧光屏上,图乙中电压的最大值U0需满足什么条件?
(3)要使荧光屏上始终显示一个完整的波形,荧光屏必须每隔多长时间回到初始位置?计算这个波形的峰值和长度.

(1)电子进入AB板时的初速度.
(2)要使所有的电子都能打在荧光屏上,图乙中电压的最大值U0需满足什么条件?
(3)要使荧光屏上始终显示一个完整的波形,荧光屏必须每隔多长时间回到初始位置?计算这个波形的峰值和长度.

分析:(1)电子经过电压为U1的加速电场加速时,电场力做功,根据动能定理求解电子进入AB板时的初速度.
(2)电子进入水平金属板A.B间后做类平抛运动,根据牛顿第二定律和运动学公式结合求出电子飞出电场时偏转距离y,当y<
时所有的电子都能打在荧光屏上,求出电压的最大值U0需满足的条件.
(3)要使荧光屏上始终显示一个完整的波形,荧光屏运动的周期应该与交变电压相同.根据三角形相似求出波形峰值与d、L、D的关系.荧光屏匀速运动,由速度公式求出长度.
(2)电子进入水平金属板A.B间后做类平抛运动,根据牛顿第二定律和运动学公式结合求出电子飞出电场时偏转距离y,当y<
| d |
| 2 |
(3)要使荧光屏上始终显示一个完整的波形,荧光屏运动的周期应该与交变电压相同.根据三角形相似求出波形峰值与d、L、D的关系.荧光屏匀速运动,由速度公式求出长度.
解答:解:
(1)设电子进入AB板时的初速度为v0
则由动能定理有eU1=
m
解得v0=
(2)电子在垂直于电场方向做匀速直线运动,运动时间t=
设电子在电场方向做匀加速直线运动的位移y=
at2=
t2
要使所有的电子都能打在荧光屏上y<
由以上各式解得U0<
(3)要使荧光屏上始终显示一个完整的波形,荧光屏运动的周期应该与交变电压的周期相同,所以,荧光屏必须每隔时间T回到初始位置.电压为峰值时荧光屏上的波形出现峰值Y.波形为正弦曲线.
该波形的峰值
=
解得Y=
所以该波形的长度S=vT
答:
(1)电子进入AB板时的初速度v0=
.
(2)要使所有的电子都能打在荧光屏上,图乙中电压的最大值U0需满足的条件是U0<
.
(3)要使荧光屏上始终显示一个完整的波形,荧光屏运动的周期应该与交变电压的周期相同,这个波形的峰值和长度分别为Y=
、S=vT
(1)设电子进入AB板时的初速度为v0
则由动能定理有eU1=
| 1 |
| 2 |
| v | 2 0 |
解得v0=
|
(2)电子在垂直于电场方向做匀速直线运动,运动时间t=
| L |
| v0 |
设电子在电场方向做匀加速直线运动的位移y=
| 1 |
| 2 |
| eU0 |
| 2md |
要使所有的电子都能打在荧光屏上y<
| d |
| 2 |
由以上各式解得U0<
| 2U1d2 |
| L2 |
(3)要使荧光屏上始终显示一个完整的波形,荧光屏运动的周期应该与交变电压的周期相同,所以,荧光屏必须每隔时间T回到初始位置.电压为峰值时荧光屏上的波形出现峰值Y.波形为正弦曲线.
该波形的峰值
| ||
|
| ||
| Y |
解得Y=
| d(L+2D) |
| 2L |
所以该波形的长度S=vT
答:
(1)电子进入AB板时的初速度v0=
|
(2)要使所有的电子都能打在荧光屏上,图乙中电压的最大值U0需满足的条件是U0<
| 2U1d2 |
| L2 |
(3)要使荧光屏上始终显示一个完整的波形,荧光屏运动的周期应该与交变电压的周期相同,这个波形的峰值和长度分别为Y=
| d(L+2D) |
| 2L |
点评:本题考查对示波器原理的理解能力.荧光屏的匀速移动与加锯齿扫描电压相似.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目