��Ŀ����
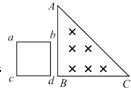
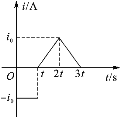
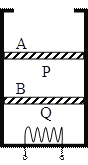
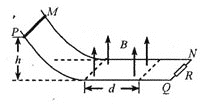
����Ŀ����ͼ��MN��PQ�ǵ��費�Ƶ�ƽ�н������죬����ΪL�������������ֹ⻬��ƽֱ���ֲִڣ�����ƽ�����ӡ��Ҷ˽�һ����ֵΪR�Ķ�ֵ���衣ƽֱ���ֵ�����������п���Ϊd��������ֱ���ϡ��Ÿ�Ӧǿ�ȴ�СΪB����ǿ�ų�������Ϊm������ҲΪR�Ľ������Ӹ߶�Ϊh����ֹ�ͷţ�����ų��ұ߽紦ǡ��ֹͣ����֪��������ƽֱ���ֵ����Ķ�Ħ������Ϊ�����������뵼���Ӵ����á�������������ų�����Ĺ�����( )
A. ������������������Ϊ![]()
B. ͨ���������ĵ����Ϊ![]()
C. �˷������������Ĺ�Ϊmgh
D. �����������Ľ�����Ϊ![]()
���𰸡�D
��������
����������������»�ʱ��ֻ��������������е���غ㣬�ɻ�е���غ㶨�ɻ��ܶ��������������������ˮƽ��ʱ���ٶȣ���E=BLv�����Ӧ�綯�ƣ�Ȼ�������Ӧ������
��![]() ���������Ӧ�������
���������Ӧ�������
�˷�����������ת��Ϊ�����ȣ��ɶ��ܶ������������غ㶨�ɣ���������˷�����������������������Ľ�������
A��������»������У���е���غ㣬�ɻ�е���غ㶨�ɵã�![]() ������������ˮƽ��ʱ���ٶ�
������������ˮƽ��ʱ���ٶ�![]() ����������ˮƽ����������˶����յ���ˮƽ��ʱ���ٶ��������Ӧ�綯��E=BLv������Ӧ����
����������ˮƽ����������˶����յ���ˮƽ��ʱ���ٶ��������Ӧ�綯��E=BLv������Ӧ����![]() ����A����
����A����
B���Ӧ�����![]() ����B����
����B����
C��������������˶������У��ɶ��ܶ����ã�mgh-WB-��mgd=0-0���˷�������������WB=mgh-��mgd����C����
D��˷�����������ת��Ϊ�����ȣ������뵼���������ȣ�ͨ�����ǵĵ�����ȣ�������������Ľ����ȣ�![]() ����D��ȷ��
����D��ȷ��
��ѡ��D��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�