Question

【题目】如图所示，倾角为37°，长为l=16 m的传送带，转动速度为v=10 m/s，动摩擦因数μ=0.5，在传送带顶端A处无初速度地释放一个质量为m=0.5 kg的物体。已知sin 37°=0.6，cos37°=0.8，g=10 m/s2。求：

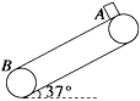
（1）传送带顺时针转动时，物体从顶端A滑到底端B的时间；

（2）传送带逆时针转动时，物体从顶端A滑到底端B的时间。

Answer 1

【答案】（1）t=4 s （2）t总=2 s

【解析】（1）传送带顺时针转动时，物体相对传送带向下运动，则物体所受滑动摩擦力沿斜面向上，相对传送带向下匀加速运动，根据牛顿第二定律有

mg（sin37°–μcos37°）=ma

则a=gsin37°–μgcos37°=2 m/s2，

根据l=at2得t=4 s。

（2）传送带逆时针转动，当物体下滑速度小于传送带转动速度时，物体相对传送带向上运动，则物体所受滑动摩擦力沿传送带向下，设物体的加速度大小为a1，由牛顿第二定律得，mgsin37°+μmgcos37°=ma1

则有a1=10 m/s2

设当物体运动速度等于传送带转动速度时经历的时间为t1，位移为x1，则有

，

x1=a1t2=5 m<l=16 m

当物体运动速度等于传送带速度瞬间，有mgsin37°>μmgcos 37°，则下一时刻物体相对传送带向下运动，受到传送带向上的滑动摩擦力。设当物体下滑速度大于传送带转动速度时物体的加速度为a2，则

x2=l–x1=11 m

又因为x2=vt2+a2t22，则有10t2+t22=11，

解得：t2=1 s （t2=–11 s舍去）

所以t总=t1+t2=2 s。