��Ŀ����
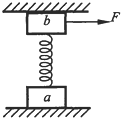
����Ŀ����ͼ��ʾ����һ����ϵ��Ϊk���ᵯ��һ�˹̶����ڱڹ⻬�İ����������ײ�![]() ��(O����)��������һ��������Ϊm��С��������С��ֹ��P��.��֪�����뾶ΪR����ˮƽ����֮��Ķ�Ħ������Ϊ
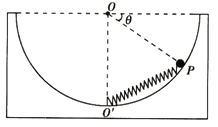
��(O����)��������һ��������Ϊm��С��������С��ֹ��P��.��֪�����뾶ΪR����ˮƽ����֮��Ķ�Ħ������Ϊ![]() ��OP��ˮƽ����ļн�Ϊ��=30�����������ٶ�Ϊg������˵����ȷ����
��OP��ˮƽ����ļн�Ϊ��=30�����������ٶ�Ϊg������˵����ȷ����
A. �ᵯ�ɶ�С�����������СΪ![]()
B. ���������ˮƽ����������˶�����
C. �����͵��ɶ�С����������ĺ�����ֱ����
D. ����ԭ��Ϊ![]()
���𰸡�CD
�������������������������С�������о���������������ð����������ܵ�����ľ�Ħ�����������С���������������֪��С����������֧���������ɵĵ��������ھ�ֹ���ɹ�������ƽ�����������С���ܵ����ᵯ�ɵĵ�����С���ܵ���֧�������ɺ��˶���������ɵ�ѹ�������������ԭ����
��������С������Ϊ�о�������������֪����ֱ�����У��������������֧���������������ˮƽ���������ƣ��������������û��Ħ������B����С����������������G�����ɵĵ���F��������֧����N����ͼ��ʾ��
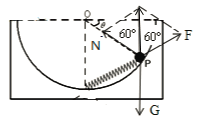
����ƽ�������������͵��ɶ�С����������ĺ���������ƽ�⣬��ֱ���ϣ���ϼ��ι�ϵ��֪![]() ��A����C��ȷ���ɺ��˶��ɣ����ɵ�ѹ����Ϊ
��A����C��ȷ���ɺ��˶��ɣ����ɵ�ѹ����Ϊ![]() ���ʵ��ɵ�ԭ��Ϊ
���ʵ��ɵ�ԭ��Ϊ![]() ��D��ȷ��
��D��ȷ��

 ��ǰ����ϵ�д�
��ǰ����ϵ�д�