题目内容
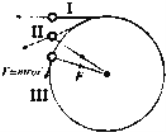
【题目】如图所示的坐标系中，第一象限内存在与x轴成30°角斜向下的匀强电场，电场强度E=400N/C；第四象限内存在垂直于纸面向里的有界匀强磁场，x轴方向的宽度OA=20 
cm），轴负方向无限大，磁感应强度B=1×10﹣4T．现有一比荷为 
=2×1011C/kg的正离子（不计重力），以某一速度v0从O点射入磁场，α=60°，离子通过磁场后刚好从A点射出，之后进入电场．
（1）求离子进入磁场B的速度v0的大小；
（2）离子进入电场后，经多少时间再次到达x轴上；
（3）若离子进入磁场B后，某时刻再加一个同方向的匀强磁场使离子做完整的圆周运动，求所加磁场磁感应强度的最小值．
【答案】
（1）解：如图所示，由几何关系得，离子在磁场中运动时的轨道半径为：r1=0.2m，
离子在磁场中做匀速圆周运动，洛伦兹力提供向心力，为：
代入数据解得： 
．
答：离子进入磁场B的速度v0的大小为4×106m/s；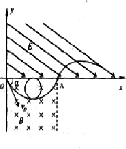 
（2）解：离子进入电场后，设经过时间t再次到达x轴上，离子沿垂直电场方向做速度为v0的匀速直线运动，位移为l1，
l1=v0t
离子沿电场方向做初速度为零的匀加速直线运动，加速度为a，位移为l2，
qE=ma
．
由几何关系可知： 
代入数据解得： 
s．
答：离子进入电场后，经 
s的时间再次到达x轴上；
（3）解：由qvB= 
知，B越小，r越大，设离子在磁场中最大半径为R，
由几何关系得： 
由牛顿运动定律得： 
得： 
则外加磁场为： 
．
答：所加磁场磁感应强度的最小值为3×10﹣4T．
【解析】（1）作出粒子的轨迹图，结合几何关系求出粒子在磁场中运动的轨道半径，根据洛伦兹力提供向心力求出离子进入磁场B的速度．
（2）离子进入电场后，速度方向与电场方向垂直，将粒子的运动分解为沿电场方向和垂直电场方向，垂直电场方向上做匀速直线运动，沿电场方向做初速度为零的匀加速直线运动，结合两个分位移的关系求出再次到达x轴上的时间．
（3）粒子在磁场中轨道半径越大，磁感应强度越小，根据几何关系得出轨道半径的最大值，结合半径公式求出磁感应强度的最小值．
