题目内容
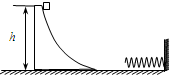
如图所示,固定的光滑竖直圆形圆形轨道,其半径为R,在它的底端静止一个质量为m小球,现给小球一个水平冲量,使小球始终不离开圆形轨道在竖直圆内运动,试求冲量应满足的条件?

I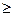
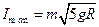 ;I
;I
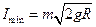
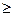
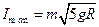 ;I
;I
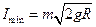
当小球运动到与竖直圆的高度为圆的半径R时速度为零,设小球的初速度为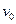 ,由机械能守恒得
,由机械能守恒得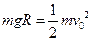 …………………… (2分)
…………………… (2分)
由动量定理得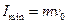 解得
解得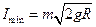 …………………… (2分)
…………………… (2分)
当小球的动量较大时,小球刚好通过最高点的速度为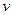 ,由牛顿第二定律可得:
,由牛顿第二定律可得: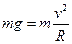 …………………… (2分)
…………………… (2分)
再由机械能守恒列式有: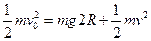 …………………… (2分)
…………………… (2分)
由动量定理得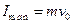
解得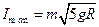 …………………… (2分)
…………………… (2分)
所以冲量I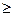
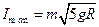 ;I
;I
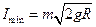 …………………… (2分)
…………………… (2分)
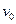 ,由机械能守恒得
,由机械能守恒得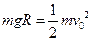 …………………… (2分)
…………………… (2分)由动量定理得
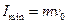 解得
解得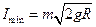 …………………… (2分)
…………………… (2分)当小球的动量较大时,小球刚好通过最高点的速度为
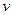 ,由牛顿第二定律可得:
,由牛顿第二定律可得: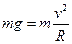 …………………… (2分)
…………………… (2分)再由机械能守恒列式有:
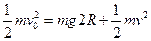 …………………… (2分)
…………………… (2分)由动量定理得
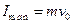
解得
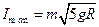 …………………… (2分)
…………………… (2分)所以冲量I
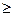
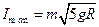 ;I
;I
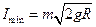 …………………… (2分)
…………………… (2分)
练习册系列答案
相关题目
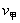 ,乙的速度
,乙的速度 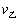 及球的速度
及球的速度 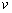 三者之间的关系为( )
三者之间的关系为( )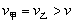
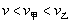
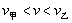
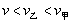
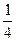
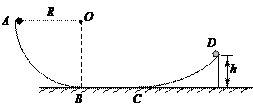
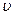 和
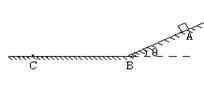
和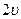 ,不计空气阻力,则两个小物体 ( )
,不计空气阻力,则两个小物体 ( )