题目内容
（18分）如图所示，在离地面H=5.45m的O处用长L=0.45m的不可伸长的细线挂一质量为0.09kg
的爆竹（火药质量忽略不计），把爆竹拉起至D点使细线水平伸直，点燃导火线后将爆竹静止释放，爆竹刚
好到达最低点B时炸成质量相等的两块，一块朝相反方向水平抛出，落到地面上的A处，抛出的水平距离
s=5m。另一块仍系在细线上继续做圆周运动，空气阻力忽略不计，取g=10m/s2，求：
（1）爆竹爆炸前瞬间的速度大小v0；
（2）继续做圆周运动的那一块在B处对细线的拉力T的大小；
（3）火药爆炸释放的能量E。
（1）3m/s （2）12.55N （3）2.88J
解析试题分析：解：（1）设爆竹的总质量为2m，爆竹从D点运动到B点过程中，
根据动能定理，得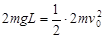
（2分）
解得
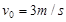（2分）
（2）设爆炸后抛出的那一块的水平速度为v1，做圆周运动的那一块的水平速度为v2。
对抛出的那一块，有：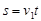
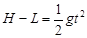（2分）
（2分）
解得v1=5m/s
对系统，根据动量守恒定律，得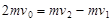
（2分）
在B处，对于做圆周运动的那一块，根据牛顿第二定律，得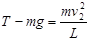
（2分）
根据牛顿第三定律，得
做圆周运动的那一块对细线的拉力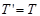
（1分）
联立以上各式，解得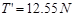
（1分）
（3）根据能量守恒定律，得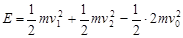
（2分）
解得E=2.88J （2分）
考点：动能定理 平抛运动 动量守恒 牛顿运动定律 能量守恒定律
名校课堂系列答案两根足够长的固定平行金属光滑导轨位于同一水平面，导轨上横放着两根相同的导体棒ab、cd与导轨构成矩形回路。导体棒的两端连接着处于压缩状态的两根轻质弹簧，两棒的中间用细线绑住，它们的电阻均为R，回路上其余部分的电阻不计。在导轨平面内两导轨间有一竖直向下的匀强磁场。开始时，导体棒处于静止状态，剪断细线后，导体棒运动过程中（ ）
| A．回路中有感应电动势 |
| B．两根导体棒所受安培力的方向相同 |
| C．两根导体棒和弹簧构成的系统机械能守恒 |
| D．两根导体棒和弹簧构成的系统机械能不守恒 |
如图所示，小球从弹簧正上方一定高度落到竖直放置在地面上的轻质弹簧上，直至速度为零，则从小球接触弹簧开始到压缩弹簧至最低点的过程中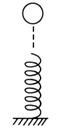 
| A．小球的动能一直减小 | B．小球的机械能一直减小 |
| C．小球的动能先增大后减小 | D．小球的机械能先增大后减小 |
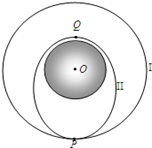
（取无穷远处引力势能为零），其中m为此时“嫦娥三号”的质量。若“嫦娥三号”在轨道II上运动的过程中，动能和引力势能相互转化，它们的总量保持不变。已知“嫦娥三号”经过Q点的速度大小为v，请根据能量守恒定律求它经过P点时的速度大小；
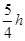）处自由下落，与斜面做无能量损失的碰撞后水平抛出．小球自由下落的落点距斜面左侧的水平距离x满足一定条件时，小球能直接落到水平地面上．
x0．求M与m的关系式。
