题目内容
【题目】如图所示，两端开口的圆筒内嵌有一凸透镜，透镜主光轴恰好与圆筒中轴线重合。为了测出该透镜的焦距以及透镜在圆筒内的位置，小李同学做如下实验：在圆筒左侧凸透镜的主光轴上放置一点光源S，在圆筒右侧垂直凸透镜的主光轴固定一光屏，点光源S与光屏的距离为L。左右移动圆筒，当圆筒左端面距离点光源S为a时，恰好在光屏上成一个清晰的像；将圆筒向右水平移动距离b，光屏上又出现了一个清晰的像。则凸透镜和圆筒左端面的距离x为____________，该透镜的焦距f为__________。
【答案】 (L-b-2a)/2 (L2-b2)/4L
【解析】试题分析：掌握凸透镜成像的规律，根据光路的可逆性，两次成像的物距和像距正好相反，即第一次的物距等于第二次的像距，第一次的像距等于第二次的物距，从而可以计算出距离x的值；根据凸透镜成像的原理，由点S发出的光经过凸透镜后会聚到像点，并结合平行于主光轴的光线过焦点分析焦距的大小．
根据光路的可逆性，第一次的物距等于第二次的像距，第一次的像距等于第二次的像距，第一次的物距
圆筒向右移动b，则凸透镜也会向右移动b，则第二次的像距为
；则
，解得
；光源S所成像应在S′处，若物体AS，则成像应为A′S′，根据成像原理，成像光路图如图所示：
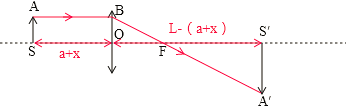
又像高与物体高度正比等于像距与物距之比，则：
，由图知，A′S′F∽BOF，则：
；AS=BO，，联立以上几式得
；
练习册系列答案
相关题目
