题目内容
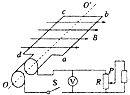
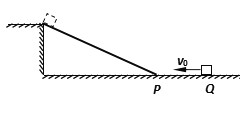
【题目】如图所示，放于竖直面内的光滑金属细圆环半径为R。质量为m的带孔小球穿于环上，同时有一长为R的细绳一端系于球上，另一端系于圆环最低点，绳能承受的最大拉力为2 mg。当圆环以角速度ω绕竖直直径转动时，发现小球受三个力作用。则ω可能为（ ）
A. 
B. 
C. 
D. 
【答案】BC
【解析】试题分析：因为圆环光滑，所以这三个力肯定是重力、环对球的弹力、绳子的拉力，细绳要产生拉力，绳要处于拉升状态，根据几何关系及向心力基本格式求出刚好不受拉力时的角速度，此角速度为最小角速度，只要大于此角速度就受三个力．
因为圆环光滑，所以这三个力肯定是重力、环对球的弹力、绳子的拉力，细绳要产生拉力，绳要处于拉升状态，根据几何关系可知，此时细绳与竖直方向的夹角为60°，当圆环旋转时，小球绕竖直轴做圆周运动，向心力由三个力在水平方向的合力提供，其大小为
，根据几何关系，其中
一定，所以当角速度越大时，所需要的向心力越大，绳子拉力越大，所以对应的第一个临界条件是小球在此位置刚好不受拉力，此时角速度最小，需要的向心力最小，对小球进行受力分析得
，即
，解得
；当绳子拉力达到2mg时，此时角速度最大，对小球进行受力分析得：竖直方向
，水平方向： 
，解得
，BC正确．
练习册系列答案
相关题目
