题目内容
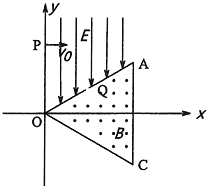
【题目】如图，OAC为正三棱柱框架在xOy平面的一个截面，OA与x轴正方向夹角为30°。OA上方空间存在沿y轴负方向、场强大小为E的匀强电场，框架内存在垂直OAC平面向外的匀强磁场。y轴上P点的离子源，每隔相同时间，以速度v0沿x轴正方向射出质量为m，电荷量为q的正离子，不考虑离子间的相互作用，离子恰好从OA正中间的小孔Q垂直于OA射入框架。若离子每次与框架内壁碰撞后等速率反弹，碰撞时间忽略不计，经过数次碰撞后又恰好从小孔Q沿与OA垂直方向射出框架，离子电荷量始终不变且离子的重力不计。已知第一个离子刚从Q处射入框架时，第二个离子恰好从P处射出，框架内磁感应强度大小不超过
。
(1)求OQ间的距离；
(2)求匀强磁场磁感应强度的大小；
(3)第一个离子从框架射出前框架内最多可能有多少个离子。
【答案】(1)
；(2)
(n=1、2、3、………,15)
【解析】(1)设离子从P到Q的时间为t1，到Q点时，速度沿y方向的分量vy，
有：
解得：
设OQ间距为L，由几何关系有，
解得：
(2)设离子在磁场中作圆周运动的半径为r，依题意有，
，其中n=0,1,2,3……
离子在磁场中运动的速度
又
，
解得，n=0,1，2,3，…，15
(3)离子在磁场中作圆周运动的周期为T，
第一个离子进入框架到离开框架经历的时间为t2，
经分析，
，其中n=0,1，2,3，…，15
解得
当n=15时该式取最大值，
所以第一个离子从框架射出前框架内最多可能有6个离子
练习册系列答案
相关题目
