题目内容
2013年12月2日1时30分，“嫦娥三号”月球探测器搭载长征三号乙火箭发射升空．该卫星在距月球表面高度为h的轨道上做匀速圆周运动，其运行的周期为T，最终在月球表面实现软着陆．若以R表示月球的半径，引力常量为G，忽略月球自转及地球对卫星的影响，下列说法不正确的是（ ）
A、“嫦娥三号”绕月运行时的向心加速度为
| ||||
B、月球的第一宇宙速度为
| ||||
C、月球的质量为
| ||||
D、物体在月球表面自由下落的加速度大小为
|
练习册系列答案
特高级教师点拨系列答案
相关题目
如图一个学生把风刮倒的旗杆绕着O点扶起来，已知旗杆的长度为L，学生的身高为h，当学生以速度v向左运动时，旗杆转动的角速度为（此时旗杆与地面的夹角为α）（ ）A、ω=
| ||
B、ω=
| ||
C、ω=
| ||
D、ω=
|
“嫦娥三号”于2013年12月14日21时11分降落在距离地球38万公里的月球上，中国成为继苏联、美国之后的第三个在月球成功实现探测器软着陆的国家．着陆前“嫦娥三号”曾在离月面100m处悬停避障，然后缓速下降，离月面4m时，7500N变推力发动机关机，“嫦娥三号”做自由落体运动降落在月球虹湾以东地区（19.51W，44.12N），已知月表重力加速度为地表重力加速度的六分之一，下列说法正确的是（g取9.8m/s2）（ ）
| A、若悬停时“嫦娥三号”的总质量为1.5×103kg，则变推力发动机的推力约为2450N | ||||
| B、“嫦娥三号”落月点的北边十几米处有一个大撞击坑，假如悬停时“嫦娥三号”在撞击坑的正上方，为避障姿态控制发动机先向南喷气，后向北喷气再次悬停在了落月点正上方 | ||||
C、变推力发动机关机后，同样的着陆速度相当于从离地球表面
| ||||
D、变推力发动机关机后，同样的着陆速度相当于从离地球表面
|
“神舟十号”飞船发射后，先进入一个椭圆轨道，经过多次变轨进入距地面高度为h的圆形轨道．已知飞船质量为m，地球半径为R，地球表面的重力加速度为g．设飞船进入圆形轨道后运动时的动能为EK，则（ ）
A、Ek=
| ||
B、Ek=
| ||
C、Ek=
| ||
| D、Ek=mgh |
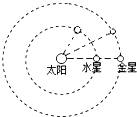把水星和金星绕太阳的运动视为圆周运动．从水星与金星和太阳在一条直线上开始计时，若测得在相同时间内水星、金星转过的角度分别为θ1、θ2（均为锐角），则由此条件可求得水星和金星（ ）| A、质量之比 | B、到太阳的距离之比 | C、绕太阳的动能之比 | D、受到的太阳引力之比 |
“嫦娥三号”月球探测器于2013年12月2日凌晨1时30分在我国西昌卫星发射基地成功发射．开启了我国“探月工程”绕、落、回计划的第二步．我国首部“月球车”--“玉兔号”成功实现软着陆．已知：地球表面的重力加速度为g，月球和地球的半径分别为R1和R2，月球和地球的质量分别为M1和M2．则下列说法正确的是（ ）
A、月球的第一宇宙速度为
| ||||||||
B、月球表面的重力加速度为
| ||||||||
C、探测器在圆轨道上绕月球飞行一周的最短时间约为2π
| ||||||||
D、月球密度为2π
|
“太空涂鸦”技术就是使低轨运行的攻击卫星在接近高轨侦查卫星时，准确计算轨道向其发射“漆雾”弹，并在临近侦查卫星时，压爆弹囊，让“漆雾”散开并喷向侦查卫星，喷散后强力吸附在侦查卫星的侦察镜头、太阳能板、电子侦察传感器等关键设备上，使之暂时失效．下列说法正确的是（ ）
| A、攻击卫星在轨运行速率大于7.9km/s | B、攻击卫星进攻前的速度比侦查卫星的速度小 | C、攻击卫星完成“太空涂鸦”后应减速才能返回低轨道上 | D、若攻击卫星周期已知，结合万有引力常亮就可计算出地球质量 |
2013年12月2日，“嫦娥三号”探测器成功发射．与“嫦娥一号”的探月轨道不同，“嫦娥三号”不采取多次变轨的形式，而是直接飞往月球，然后再进行近月制动和实施变轨控制，进入近月椭圆轨道．现假定地球、月球都静止不动，用火箭从地球沿地月连线向月球发射一探测器，探测器在地球表面附近脱离火箭．已知地球中心与月球中心之间的距离约为r=3.8×105km，月球半径R=1.7×103km，地球的质量约为月球质量的81倍，在探测器飞往月球的过程中（ ）
| A、探测器到达月球表面时动能最小 | B、探测器距月球中心距离为3.8×104km时动能最小 | C、探测器距月球中心距离为3.42×105km时动能最小 | D、探测器距月球中心距离为1.9×105km时动能最小 |
如图所示，B为绕地球做椭圆轨道运行的卫星，椭圆的半长轴为a，运行周期为TB；C为绕地球做圆周运动的卫星，圆周的半径为r，运行周期为TC；P为B、C两卫星轨道的交点．下列说法或关系式中正确的是（ ）A、
| ||||
B、
| ||||
| C、卫星B在P点的加速度与卫星C在该点加速度一定相同 | ||||
| D、若卫星C为近地卫星，且已知C的周期和万有引力常量，则可求出地球的平均密度 |