题目内容
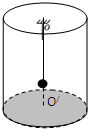 如图所示,一个光滑圆筒立于水平桌面上,圆筒的直径为L.一条长度也为L的细绳一端固定在圆筒中心线上的O点,另一端拴着一个质量为m的小球(可视为质点).小球以速率v绕中心线OO′在水平面内做匀速圆周运动,但球不会碰到筒底.试求:
如图所示,一个光滑圆筒立于水平桌面上,圆筒的直径为L.一条长度也为L的细绳一端固定在圆筒中心线上的O点,另一端拴着一个质量为m的小球(可视为质点).小球以速率v绕中心线OO′在水平面内做匀速圆周运动,但球不会碰到筒底.试求:(1)当v1=
|
(2)当v2=
|
分析:(1)先根据牛顿第二定律求出球刚好挨着内壁作匀速圆周运动的临界速度v0,再根据v1与v0的关系,确定向心力的来源,由牛顿第二定律求解.
(2)v2>v0时,小球紧挨着内壁作匀速圆周运动,受到重力、细绳的拉力和筒壁的弹力,其合力提供向心力,列式求解绳对小球的拉力T2和圆筒壁对小球的支持力N2.
(2)v2>v0时,小球紧挨着内壁作匀速圆周运动,受到重力、细绳的拉力和筒壁的弹力,其合力提供向心力,列式求解绳对小球的拉力T2和圆筒壁对小球的支持力N2.
解答:解:设球刚好挨着内壁作匀速圆周运动的速度为v0.此时由重力和细绳的拉力的合力提供向心力,则有:
mgtan30°=m
解得:v0=
(1)当v1=
时,时,因为v1<v0,所以小球没有贴着筒壁而做半径较小的圆周运动,圆筒壁对小球的支持力N1=0.
设此时绳与竖直方向夹角为α,
则:T1sinα=m
T1cosα=mg,
解得:T1≈1.09mg
(2)当v2=
时,因为v2>v0,所以小球紧挨着内壁作匀速圆周运动,受到重力、细绳的拉力和筒壁的弹力,其合力提供向心力,则得:
竖直方向有:T2cosα=mg
水平方向有:T2sinα+N2=m
解得:T2=1.15 mg,N2=1.15 mg.
答:(1)当v1=
时,绳对小球的拉力T1是1.09mg,圆筒壁对小球的支持力N1为0.
(2)当v2=
时,绳对小球的拉力T2是1.15 mg,圆筒壁对小球的支持力N2是1.85 mg.
mgtan30°=m
| ||
| Lsin30° |
解得:v0=
|
(1)当v1=
|
设此时绳与竖直方向夹角为α,
则:T1sinα=m
| v2 |
| Lsinα |
T1cosα=mg,
解得:T1≈1.09mg
(2)当v2=
|
竖直方向有:T2cosα=mg
水平方向有:T2sinα+N2=m
| ||
| Lsinα |
解得:T2=1.15 mg,N2=1.15 mg.
答:(1)当v1=
|
(2)当v2=
|
点评:本题要注意判断筒壁对球有无弹力,分析向心力来源,再运用牛顿第二定律求解.

练习册系列答案
相关题目
 某游乐场开发了一个名为“翻天滚地”的游乐项目.原理图如图所示:一个
某游乐场开发了一个名为“翻天滚地”的游乐项目.原理图如图所示:一个| 3 |
| 4 |
A、要使球能从C点射出后能打到垫子上,则球经过C点时的速度至少为
| ||
| B、球从A到B的过程中重力的功率先减小后增大 | ||
C、若球从C点射出后恰好能打到垫子的M端,则球经过C点时对管外壁压力大小为
| ||
| D、要使球能通过C点落到垫子上,球离A点的最大高度是5R |
 如图所示,一个光滑的圆锥体固定在水平圆盘上,其轴线沿竖直方向并与圆盘中心重合,母线与轴线间的夹角为θ.一条长为l的细绳,一端固定在圆锥体的顶点O处,另一端拴着一质量为m的小球(可视为质点).现让圆锥体绕其中心轴线由静止开始转动,求当其角速度由零增大到
如图所示,一个光滑的圆锥体固定在水平圆盘上,其轴线沿竖直方向并与圆盘中心重合,母线与轴线间的夹角为θ.一条长为l的细绳,一端固定在圆锥体的顶点O处,另一端拴着一质量为m的小球(可视为质点).现让圆锥体绕其中心轴线由静止开始转动,求当其角速度由零增大到 如图所示,一个
如图所示,一个 如图所示,一个
如图所示,一个 如图所示,一个
如图所示,一个