题目内容
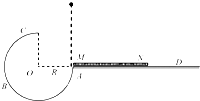 如图所示,一个
如图所示,一个| 3 | 4 |
分析:根据重力提供向心力求出小球经过C点的最小速度,然后根据平抛运动知识求出射程;在根据恰好射到N点得到经过C点的最大速度;最后根据机械能守恒定律求初位置高度.
解答:解:小球能通过C点,在C点最小速度v满足:
mg=m
解得
v=
小球离开C点做平抛运动,落到M点时间t为:
t=
此时水平距离:x=vt=
R>R,小球能落在垫子上
小球在C点的最大速度为v′:
4R=v′t
解得
v′=2
设小球距离A点的高度为h,则小球运动到C点的过程中,有
mg(h-R)=
m
由上可知,要使小球落在垫子上:
≤vC≤
解得:
R≤vC≤5R
即小球能从C点射出并打到垫子上,小球距离A点的高度范围是
R≤vC≤5R.
mg=m
| v2 |
| R |
解得
v=
| gR |
小球离开C点做平抛运动,落到M点时间t为:
t=
|
此时水平距离:x=vt=
| 2 |
小球在C点的最大速度为v′:
4R=v′t
解得
v′=2
| 2gR |
设小球距离A点的高度为h,则小球运动到C点的过程中,有
mg(h-R)=
| 1 |
| 2 |
| v | 2 C |
由上可知,要使小球落在垫子上:
| gR |
| 8gR |
解得:
| 3 |
| 2 |
即小球能从C点射出并打到垫子上,小球距离A点的高度范围是
| 3 |
| 2 |
点评:本题关键根据小球能通过C点,以及要落在垫子上求出小球经过C点的速度范围,然后根据机械能守恒定律求解初位置的高度.

练习册系列答案
相关题目
 某游乐场开发了一个名为“翻天滚地”的游乐项目.原理图如图所示:一个
某游乐场开发了一个名为“翻天滚地”的游乐项目.原理图如图所示:一个| 3 |
| 4 |
A、要使球能从C点射出后能打到垫子上,则球经过C点时的速度至少为
| ||
| B、球从A到B的过程中重力的功率先减小后增大 | ||
C、若球从C点射出后恰好能打到垫子的M端,则球经过C点时对管外壁压力大小为
| ||
| D、要使球能通过C点落到垫子上,球离A点的最大高度是5R |
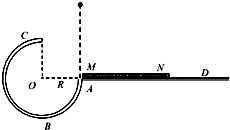 如图所示,一个
如图所示,一个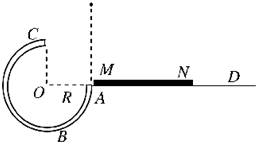 如图所示,一个
如图所示,一个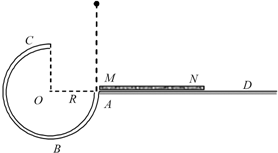 如图所示,一个
如图所示,一个