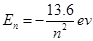题目内容
 已知氢原子基态的电子轨道半径为r1=0.528×10-10m,量子数为n的能级值为EN=-
已知氢原子基态的电子轨道半径为r1=0.528×10-10m,量子数为n的能级值为EN=-| 13.6ev | n2 |
(1)求电子在基态轨道上运动时的动能.
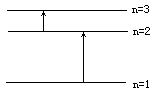
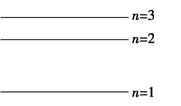
(2)有一群氢原子处于量子数n=3的激发态.画一能级图,在图上用箭头标明这些氢原子能发出哪几条光谱线.
(3)计算这几条光谱线中波长最短的一条的波长.
(4)若要使处于基态的氢原子电离,至少要用多大频率的电磁波照射原子.(其中静电力恒量K=9.0×109N?m2/C2,电子电量e=1.6×10-19C,普朗克恒量h=6.63×10-34J?s,真空中光速c=3.0×108m/s).
分析:(1)根据牛顿第二定律,结合库仑定律与动能表达式,即可求解;
(2)一群氢原子处于量子数n=3的激发态从低能级跃迁时,发出不同频率的光谱线;
(3)根据跃迁的能级差值,结合△E=
,即可求解;
(4)根据电离的概念,结合γ=
,即可求解.
(2)一群氢原子处于量子数n=3的激发态从低能级跃迁时,发出不同频率的光谱线;
(3)根据跃迁的能级差值,结合△E=
| hc |
| λ |
(4)根据电离的概念,结合γ=
| △E |
| h |
解答:解: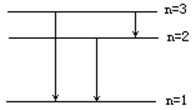 (1)设电子的质量为m,电子在基态轨道上的速率为v1,
(1)设电子的质量为m,电子在基态轨道上的速率为v1,
根据牛顿第二定律和库仑定律有m
=
∴Ek=
mv12=
=
=2.18×10-18(J)=13.6(eV)
(2)当氢原子从量子数n=3的能级跃迁到较低能级时,可以得到3条光谱线.
(3)与波长最短的一条光谱线对应的能级差为E3-E1.
λ=
=
=1.03×10-7m
(4)欲使氢原子电离,即将电子移到离核无穷远处,此处E∞=0,
故△E≥E∞-E1=0-(-13.6 eV)=13.6 eV
对应光子的最小频率应为:ν=
=3.28×1015 Hz.
答:(1)电子在基态轨道上运动时的动能13.6(eV).
(2)有一群氢原子处于量子数n=3的激发态.画一能级图,在图上用箭头标明这些氢原子能发出3条光谱线,如图所示.
(3)计算这几条光谱线中波长最短的一条的波长是1.03×10-7m.
(4)若要使处于基态的氢原子电离,至少要用3.28×1015 Hz频率的电磁波照射原子.
 (1)设电子的质量为m,电子在基态轨道上的速率为v1,
(1)设电子的质量为m,电子在基态轨道上的速率为v1,根据牛顿第二定律和库仑定律有m
| ||
| r1 |
| Ke2 | ||
|
∴Ek=
| 1 |
| 2 |
| Ke2 |
| 2r1 |
| 9.0×109×(1.6×10-19)2 |
| 2×0.528×10-10 |
(2)当氢原子从量子数n=3的能级跃迁到较低能级时,可以得到3条光谱线.
(3)与波长最短的一条光谱线对应的能级差为E3-E1.
λ=
| hc |
| E3-E1 |
| 6.63×10-34×3×108 |
| [-1.5-(-13.6)]×1.6×10-19 |
(4)欲使氢原子电离,即将电子移到离核无穷远处,此处E∞=0,
故△E≥E∞-E1=0-(-13.6 eV)=13.6 eV
对应光子的最小频率应为:ν=
| △E |
| h |
答:(1)电子在基态轨道上运动时的动能13.6(eV).
(2)有一群氢原子处于量子数n=3的激发态.画一能级图,在图上用箭头标明这些氢原子能发出3条光谱线,如图所示.
(3)计算这几条光谱线中波长最短的一条的波长是1.03×10-7m.
(4)若要使处于基态的氢原子电离,至少要用3.28×1015 Hz频率的电磁波照射原子.
点评:考查牛顿第二定律与库仑定律的应用,掌握△E=
的应用,理解电离的含义,同时注意正确的计算.
| hc |
| λ |

练习册系列答案
相关题目