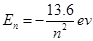Question

已知氢原子基态的电子轨道半径为r0=0.528×10-10m，量子数为n的能级值En=-

13.6eV

n2

．求：
（1）电子在基态轨道上运动的动能；
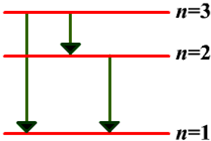
（2）有一群氢原子处于量子数n=3的激发态，画一能级图，在图上用箭头标明这些氢原子能发出哪几条光谱线？
（3）计算这几条光谱线中波长最短的一条谱线（k=9.0×10⁹N?m²/C²，e=1.60×10^-19C，h=6.63×10^-34J?s）

Answer 1

分析：1、根据库仑引力提供向心力求出电子在基态轨道上运动的速率，再求出动能
2、根据高能级跃迁到低能级画图
3、波长最短，即频率最大，能级间发生跃迁时吸收或辐射的光子能量等于两能级间的能级差．

解答：解：①根据库仑引力提供向心力得

k e 2

r 2 0

=m

v 2

r   0

，
则

1

2

m

v

2

=

1

2

k e 2

r   0

=13.6ev
②画一能级图，

③根据λ=

C

γ

λ最小，频率最大．
n=1到n=3，λ=λ=

hc

( E   3 - E   1 )

=1.03×1

0

-7

m
答：（1）电子在基态轨道上运动的动能是13.6eV；
（2）如图
（3）波长最短的一条谱线波长是1.03×^-7m

点评：解决本题的关键知道能级间跃迁所满足的规律，即E_m-E_n=hv．