题目内容
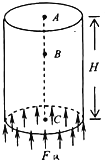
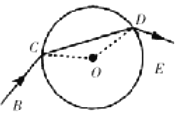
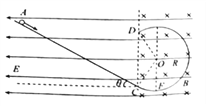
【题目】在如图所示的正交电磁场中竖直固定着一个半径R=![]() m的光滑圆弧,圆弧CD竖直固定,它对应的圆心角为240°,在C的左端有一倾斜的切线光滑轨道AC与水平面夹角θ=30°,电场强度为E的电场充满整个空间,而磁感应强度为B的磁场只分布在圆弧轨道所在的右半侧区域,已知E和B在数值上相等,取重力加速度g=10m/s2。现在A点安装一个弹射装置,它能以不同速度沿AC方向发射可视为质点的带电小球,小球的质量为m,小球射出后能在AC上做匀速直线运动,则下列说法正确的是
m的光滑圆弧,圆弧CD竖直固定,它对应的圆心角为240°,在C的左端有一倾斜的切线光滑轨道AC与水平面夹角θ=30°,电场强度为E的电场充满整个空间,而磁感应强度为B的磁场只分布在圆弧轨道所在的右半侧区域,已知E和B在数值上相等,取重力加速度g=10m/s2。现在A点安装一个弹射装置,它能以不同速度沿AC方向发射可视为质点的带电小球,小球的质量为m,小球射出后能在AC上做匀速直线运动,则下列说法正确的是
A. 小球一定带负电
B. 小球在轨道的最低点F处速度最大
C. 让小球以初速度![]() 射出,则小球不会脱离轨道
射出,则小球不会脱离轨道
D. 若撤去磁场,让小球以初速度![]() 射出,则小球一定不会脱离轨道
射出,则小球一定不会脱离轨道
【答案】D
【解析】小球在AC上匀速直线运动时,受竖直向下的重力,垂直轨道的支持力和电场力作用,由平衡条件知电场力只能向左,即小球带正电,否则不可能匀速运动,故A项错误;小球匀速运动时由![]() 和
和![]() 知
知![]() ,由几何关系知C点是圆轨道上的物理最低点,即小球运动到C点时速度最大,故B项错误;CO的延长线与轨道的交点是物理的最高点,设为P,则只要小球能过P点就不会脱离轨道。设小球在P点的速度为v,则有
,由几何关系知C点是圆轨道上的物理最低点,即小球运动到C点时速度最大,故B项错误;CO的延长线与轨道的交点是物理的最高点,设为P,则只要小球能过P点就不会脱离轨道。设小球在P点的速度为v,则有![]() ,代入数据得
,代入数据得![]() ,而由
,而由![]() 知小球从C点到P点的过程中一定要克服重力和电场力做功,即初速度
知小球从C点到P点的过程中一定要克服重力和电场力做功,即初速度![]() 时才能不脱离轨道,故C项错误;若撤去磁场后,设小球恰好在圆弧中转过90°时速度为
时才能不脱离轨道,故C项错误;若撤去磁场后,设小球恰好在圆弧中转过90°时速度为![]() ,由动能定理得
,由动能定理得![]() 知
知![]() ,因
,因![]() ,故小球在圆弧上尚未运动到90°的角度就沿圆弧轨道返回,因此是不可能脱离轨道的,故D项正确。
,故小球在圆弧上尚未运动到90°的角度就沿圆弧轨道返回,因此是不可能脱离轨道的,故D项正确。

练习册系列答案
相关题目