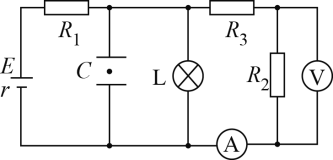
题目内容
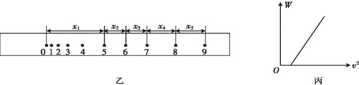
【题目】在绝缘粗糙的水平面上相距为6L的A、B两处分别固定正点电荷,其电量分别为QA、QB,两点电荷的位置坐标如图甲所示.图乙是A、B连线之间的电势φ与位置x之间的关系图像,图中x=L点为图线的最低点,若将质量为m、电荷量为+q的带电小球(可视为质点)在x=2L的C点由静止释放,其向左运动,则在接下来的过程中,下列说法正确的是
![]()

A.小球一定能到达x= - 2L点处
B.小球在x=L处的加速度最小
C.小球在向左运动过程中动能先增大后减小
D.电量QA∶QB=2∶1
【答案】C
【解析】
A.若水平面光滑根据动能定理得qU=0,知U=0,所以小球能运动到电势与出发点的电势相等的位置,由于x=-2L处的电势高于x=2L,所以不能到达x=-2L点处,根据能量守恒定律可知,若水平面粗糙,则小球到达最左端的位置会比光滑时的还要近,故A错误;
BC.据φ-x图像切线的斜率等于场强E,则知x=L处场强为零,所以在C处场强向左,小球向左加速运动,由于在运动过程中受到摩擦力,且摩擦力向右,大小不变,故在x=L右侧某位置,合力为零,此时速度最大,加速度最小,所以小球向做加速运动后做减速运动,故动能先增大后减小,故B错误,C正确;
D.x=L处场强为零,根据点电荷场强则有
![]()
解得
![]()
故D错误.

练习册系列答案
相关题目