Question

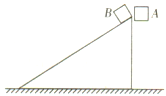
【题目】如图所示，一质量为m的物体在沿斜面向上的恒力F作用下，由静止从底端向上做匀加速直线运动．若斜面足够长，表面光滑，倾角为θ．经时间t恒力F做功80J，此后撤去恒力F，物体又经时间t回到出发点，且回到出发点时的速度大小为v，若以地面为重力势能的零势能面，则下列说法中正确的是（　　）

A.物体回到出发点时的机械能是80 J
B.在撤去力F前的瞬间，力F的功率是 mgvsinθ
C.撤去力F前的运动过程中，物体的重力势能一直在增加，撤去力F后的运动过程中物体的重力势能先增加再减少
D.撤去力F前的运动过程中，物体的动能一直在增加，撤去力F后的运动过程中物体的动能一直在减少

Answer 1

【答案】A,B,C
【解析】解：A、根据功能原理知，除了重力之外的力对物体做正功时，物体的机械能就要增加，增加的机械能等于外力作功的大小，由于拉力对物体做的功为80J，所以物体的机械能要增加80J，撤去拉力之后，物体的机械能守恒，所以物体回到出发点时的机械能是80J，A符合题意．

B、设撤去力F前和撤去力F后的运动过程中物体的加速度大小分别为：a1和a2．这两个过程的位移大小相等，方向相反，取沿斜面向上为正方向，则有：

a1t2=﹣（a1tt﹣ a2t2），则得，a1：a2=1：3．

因为物体做匀加速直线运动，初速度为0，由牛顿第二定律可得：F﹣mgsinθ=ma1，

撤去恒力F后是匀变速运动，且加速度为：a2=gsinθ

联立上两式得：F= mgsinθ

设刚撤去拉力F时物体的速度大小为v′，则有：v′=a1t= gsinθt

对于从撤去到返回的整个过程，有：﹣v=v′﹣gsinθt，

解得，v′= v，所以在撤去力F前的瞬间，力F的功率：P=Fv′= mgvsinθ，B符合题意．

C、撤去力F前的运动过程中，物体一直上升，重力势能一直在增加．撤去力F后，物体先上升后下滑，物体的重力势能先增加再减少，C符合题意．

D、撤去力F前的运动过程中，物体做匀加速运动，动能一直在增加，撤去力F后的运动过程中，物体先向上减速，后向下加速，所以动能先减少后增加，D不符合题意．

所以答案是：ABC

【考点精析】本题主要考查了功能关系的相关知识点，需要掌握当只有重力（或弹簧弹力）做功时，物体的机械能守恒；重力对物体做的功等于物体重力势能的减少:W G =E p1 -E p2；合外力对物体所做的功等于物体动能的变化:W 合 =E k2 -E k1 （动能定理）；除了重力（或弹簧弹力）之外的力对物体所做的功等于物体机械能的变化:W F =E 2 -E 1才能正确解答此题．