��Ŀ����
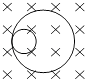
����Ŀ����ͼ��ʾ���̶���O��ϵһ��L=0.6m��ϸ����ϸ�����¶�ϵһ����m=1.0kg��С����Ϊ�ʵ㣩��ԭ�����ھ�ֹ״̬������ƽ̨��B��Ӵ�����ƽ̨��ѹ����ƽ̨��h=0.80m��һ����M=2.0kg����鿪ʼ��ֹ��ƽ̨�ϵ�P�㣬�ֶ�Mʩ��һˮƽ���ҵij��ٶ�V0 �� ���M�شֲ�ƽ̨���������˶���ƽ̨��ԵB����С��m��������������С��m������Լ������Բ���˶�������ߵ�Aʱ�����ϵ�����ǡ�õ��ڰ������������M����ˮƽ�����ϵ�C�㣬��ˮƽλ��S=1.2m�����ƿ���������g=10m/s2 �� ��
��1������ΪM������ʱ�ٶȴ�С��
��2����ƽ̨���������䶯Ħ��������=0.5�����M��С��ij�ʼ����ΪS1=1.3m�����M��P���ij��ٶȴ�СΪ���٣�
���𰸡�
��1���⣺�������M��ƽ���˶������� ƽ���˶��ij��ٶ�ΪV3
![]() ����
����
S=V3t ����
�ã� ![]() =3.0 m/s ����
=3.0 m/s ����
���ʱ����ֱ�ٶ�Ϊ�� ![]() =4.0 m/s ����
=4.0 m/s ����
����������ʱ���ٶȴ�С�� ![]() =5.0 m/s ����
=5.0 m/s ����
��2���⣺�����С����B����ײ������ײǰ�����ٶ�ΪV1����ײ��С����ٶ�ΪV2���ɶ����غ㶨�ɣ�
MV1=mV2+MV3 ����
����С���B���˶�����ߵ�A�����л�е���غ㣬��С����A����ٶ�ΪVA��
![]() ����
����
С������ߵ�ʱ����������У� ![]() ����
����
�ɢߢ��ã�V2=6.0 m/s ����
�ɢۢޢ�ã� ![]() =6.0 m/s ����
=6.0 m/s ����
���M��P�˶���B�������У��ɶ��ܶ�����
![]()
��ã� ![]() =7.0 m/s
=7.0 m/s
����������1��ƽ���˶���ˮƽ������������ֱ���˶�������ֱ�����������������˶�������ˮƽ�����Ϻ���ֱ�����ϵ��˶������������ΪM��������ʱ���ٶȴ�С����2������ţ�ٵڶ����ɺͻ�е���غ㶨�������ײ��B����ٶȣ�����ƽ���˶��ó�M������ٶȣ���϶����غ㶨�������ײǰM����B����ٶȣ����ݶ��ܶ���������M��P���ij��ٶȴ�С��
�����㾫�����������⣬������Ҫ�˽�ƽ���˶�(�ص�:�پ���ˮƽ����ij��ٶ�;��ֻ���������ã��Ǽ��ٶ�Ϊ�������ٶ�g���ȱ��������˶����˶�����:ƽ���˶����Էֽ�Ϊˮƽ���������ֱ���˶�����ֱ��������������˶�)����Ҫ���ն��ܶ���������(���ܶ����ı���ʽ���������ܺ�����������ֱ���˶�������µó���.����Ҳ�����ڱ����������������˶�����������Ͷ��ܶ��DZ�������������ʸ������ֽ⣬�ʶ��ܶ�������ʽ)�����֪ʶ���Ǵ���Ĺؼ���

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д� Ŀ�����ϵ�д�
Ŀ�����ϵ�д�