题目内容
15. 如图所示,倾角为37°的粗糙斜面的底端有一质量m=1kg的凹形小滑块,小滑块与斜面间的动摩擦因数μ=0.25.现让小滑块以某一初速度v从斜面底端上滑,同时在斜面底端正上方有一小球以初速度v0水平抛出,经过0.4s,小球恰好垂直斜面方向落入凹槽,此时,小滑块还在上滑过程中.已知sin 37°=0.6,cos 37°=0.8,g=10m/s2,求:
如图所示,倾角为37°的粗糙斜面的底端有一质量m=1kg的凹形小滑块,小滑块与斜面间的动摩擦因数μ=0.25.现让小滑块以某一初速度v从斜面底端上滑,同时在斜面底端正上方有一小球以初速度v0水平抛出,经过0.4s,小球恰好垂直斜面方向落入凹槽,此时,小滑块还在上滑过程中.已知sin 37°=0.6,cos 37°=0.8,g=10m/s2,求:(1)小球水平抛出的速度v0;
(2)小滑块的初速度v.
分析 (1)根据运动时间可以求出平抛小球竖直方向速度,根据水平和竖直速度关系可以求出平抛小球的初速度;
(2)滑块沿斜面减速上划,根据牛顿第二定律求出其加速度,然后求出其位移可正确解答本题.
解答 解:(1)设小球落入凹槽时竖直速度为vy,则有:
vy=gt=10×0.4=4m/s
因此有:v0=vytan37°=3m/s.
(2)小球落入凹槽时的水平位移:x=v0t=3×0.4=1.2m.
则滑块的位移为:$s=\frac{x}{cos37°}=\frac{1.2}{0.8}=1.5m$,
根据牛顿第二定律,滑块上滑的加速度为:
a=gsin37°+μgcos37°=8m/s2
根据公式:$s=vt-\frac{1}{2}a{t}^{2}$
:v=5.35m/s.
答:(1)小球水平抛出的速度为3m/s;
(2)小滑块的初速度为5.35m/s.
点评 该题考查了学生对多物体、多过程问题的理解分析能力,解决这类问题的关键是正确分析每个运动过程,正确应用所学知识求解.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
3.下列说法中正确的是( )
| A. | 任何带电体所带电荷的多少一定是元电荷的整数倍 | |
| B. | 沿电场线的方向电场强度越来越小 | |
| C. | 电场中某点的电场强度的方向与放入电场中该点的电荷的正负电性有关 | |
| D. | 电场中的电场线可能相交 |
4. 简谐波在t=0.8s时的图象如图甲所示,其x=0处质点的振动图象如图乙所示,由图象可知下列说法正确的是( )
简谐波在t=0.8s时的图象如图甲所示,其x=0处质点的振动图象如图乙所示,由图象可知下列说法正确的是( )
 简谐波在t=0.8s时的图象如图甲所示,其x=0处质点的振动图象如图乙所示,由图象可知下列说法正确的是( )
简谐波在t=0.8s时的图象如图甲所示,其x=0处质点的振动图象如图乙所示,由图象可知下列说法正确的是( )| A. | 波沿x 轴正方向传播 | |
| B. | 波沿x 轴负方向传播 | |
| C. | 波速为5m/s | |
| D. | 经9.2s,x=4m 处质点的位移为0.05m | |
| E. | 经9.2s,x=4m 处质点的位移为-0.05m |
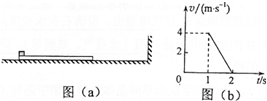 一长木板置于粗糙水平地面上,木板左端放置一小物块;在木板右方有一墙壁,木板右端与墙壁的距离为4.5m,如图(a)所示.t=0时刻开始,小物块与木板一起以共同速度向右运动,直至t=1s时木板与墙壁碰撞(碰撞时间极短).碰撞前后木板速度大小不变,方向相反;运动过程中小物块始终未离开木板.已知碰撞后1s时间内小物块的v-t图线如图(b)所示.木板的质量是小物块质量的15倍,重力加速度大小g取10m/s2.求
一长木板置于粗糙水平地面上,木板左端放置一小物块;在木板右方有一墙壁,木板右端与墙壁的距离为4.5m,如图(a)所示.t=0时刻开始,小物块与木板一起以共同速度向右运动,直至t=1s时木板与墙壁碰撞(碰撞时间极短).碰撞前后木板速度大小不变,方向相反;运动过程中小物块始终未离开木板.已知碰撞后1s时间内小物块的v-t图线如图(b)所示.木板的质量是小物块质量的15倍,重力加速度大小g取10m/s2.求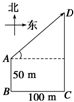 如图所示,某人从学校的门口A处开始散步,先向南走了50m到达B处,再向东走了100m到达C处,最后又向北走了150m到达D处,则A、B、C、D各点位置如何表示?
如图所示,某人从学校的门口A处开始散步,先向南走了50m到达B处,再向东走了100m到达C处,最后又向北走了150m到达D处,则A、B、C、D各点位置如何表示?