��Ŀ����
����Ŀ����ͼ��ʾ,����Ϊm��0.2kg��С��(����Ϊ�ʵ�)��ˮƽ�����Ҷ˵�A�Գ��ٶ�v0ˮƽ�׳�,�����Ҳ���һ��ֱ���õĹ⻬���MNP,��Ϊ�뾶R��0.8m��Բ����ȥ�����Ͻ�135����Բ��,MNΪ����ֱֱ��.P�㵽�������ֱ����ΪR.С����������ǡ��P������ײ������Բ���, gȡ10 m/s2.
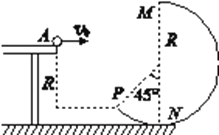
(1)��С����A��ij��ٶ�v0��AP���ˮƽ����x;
(2)��С��Բ�����͵�Nʱ��N���ѹ��;
���𰸡���1��![]() ��
��![]() ��2��
��2��![]() ��ֱ����
��ֱ����
��������
��1����С����P���ٶȷֽ⣬�ҳ�P��ˮƽ���ٶ�����ֱ���ٶȼ��ϵ���ٶ�С���A��P��ƽ���̷������С����A��ij��ٶ�v0��AP���ˮƽ����x����2�����ٶȵĺϳ����С����P���ٶȣ�Ӧ�û�е���غ����С����N���ٶȣ���С����N��������������ţ�ٵڶ�������С����N���ܵ�֧�������پ�ţ�ٵ����������С��Բ�����͵�Nʱ��N���ѹ����
��1�������A����ƽ���˶�����P��ǡ����Բ��������߽��������������P����ٶ���ˮƽ�����450б���£����ٶȷֽ��ˮƽ�����![]() ����ֱ�����
����ֱ�����![]() �ɵã�
�ɵã�
![]() ����ã�
����ã�![]()
��С���A��P��ƽ���̣�![]() ��
��![]() ��
��![]()
������ã�![]() ��
��![]()
��2�������P����ٶ�![]()
С���P�㵽N�㣬�ɻ�е���غ�ã�![]()
С����N�㣬��ţ�ٵڶ����ɵ�![]()
�������ݽ��С������֧����FN=9.17N
��ţ�ٵ������ɵã�С���N���ѹ��ΪF'N=9.17 N��������ֱ������

 �п������п��Ծ����ϵ�д�
�п������п��Ծ����ϵ�д� ��������״Ԫ��ϵ�д�
��������״Ԫ��ϵ�д� �ƸԿ�����ҵ��ϵ�д�
�ƸԿ�����ҵ��ϵ�д�