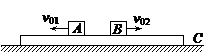题目内容
 如图,有一固定长度的木板C放在光滑水平面上,木板上面放置可视为质点的木块A、B,A、B、C的质量均相等.木块A、B相距0.2m,放在木板上适当的位置,它们与木板间的动摩擦因数相同均为μ=0.2,两物块均在同一直线上,开始时都处于静止状态.某时刻同时使物体A、B分别以速度v01=3m/s、v02=1m/s向相反方向运动,g取10m/s2,如图所示.问:
如图,有一固定长度的木板C放在光滑水平面上,木板上面放置可视为质点的木块A、B,A、B、C的质量均相等.木块A、B相距0.2m,放在木板上适当的位置,它们与木板间的动摩擦因数相同均为μ=0.2,两物块均在同一直线上,开始时都处于静止状态.某时刻同时使物体A、B分别以速度v01=3m/s、v02=1m/s向相反方向运动,g取10m/s2,如图所示.问:(1)在A、B同时运动的过程中,木板C的运动状态应该怎样?
(3)若A、B最终不滑离木板,最后它们的共同速度为多少?
(2)若要使A、B最终不滑离木板,木板C的长度至少为多少?
分析:A、B与木板间滑动摩擦力的大小相等,A、B木块分别向左、向右做匀加速运动,A、B对木板C的摩擦力大小相同,方向相反.
由动量守恒定律求得最后它们的共同速度.
在F1、F2作用下分别求出A、B的加速度,进而求出撤去外力时AB的位移和速度,撤去这两个力后,A、B的加速度大小相等,分别求出AB停止运动的时间,和运动的位移,根据位移之间的关系即可求解.
由动量守恒定律求得最后它们的共同速度.
在F1、F2作用下分别求出A、B的加速度,进而求出撤去外力时AB的位移和速度,撤去这两个力后,A、B的加速度大小相等,分别求出AB停止运动的时间,和运动的位移,根据位移之间的关系即可求解.
解答:解:(1)A、B与木板间滑动摩擦力的大小相等,A、B木块分别向左、向右做匀加速运动,A、B对木板C的摩擦力大小相同,方向相反,
所以在A、B同时向相反方向运动的过程中,木板C保持静止.
(2)由动量守恒定律得:mv01-mv02=3mv
得v=
(m/s)
(3)A、B的加速度大小相等,aA=aB=μg=2m/s2
B先相对于C静止,运动时间t1=
=0.5s,
此时A的速度,vA1=vA-aA′t1=2m/s
这段时间C一直保持静止状态,A、B的位移分别为:sA=vAt -
aA
=
m
sB=
vBt=
m
以后B相对于木板静止,A继续减速运动,木板的加速度:
ac=
=1(m/s)
设此后A与木板的相对运动时间为t2,
vA1-aA′t2=act2
t2=
(s)
在t2时间内,A与木板相对运动距离△s=
(m)
木板的最小长度 s=s0+s1+s2+s3=2.37(m)
另一种方法:直接用动量守恒定律和能量转化方程.
由动量守恒定律得:mv01-mv02=3mv
得v=
(m/s)
当B相对地速度为0后,BC一起向左加速,直至三者速度相等.
当vB=0时,由动量守恒定律得:mv01-mv02=mv1+0
得:v1=2m/s
因为
=
(m/s),
=
(m/s),
所以s1=2 s2
由能量关系得:
m(
+
)-
m
=μmg(s1+s2)
得:s1=1.25(m),s2=0.25(m)
BC相对静止后,
m
-
3m
=μmgs3
s3=
(m)
L=s0+s1+s2+s3=2.37(m)
答:(1)在A、B同时运动的过程中,木板C保持静止
(2)若A、B最终不滑离木板,最后它们的共同速度为
(m/s)
(3)若要使A、B最终不滑离木板,木板C的长度至少为2.37(m)
所以在A、B同时向相反方向运动的过程中,木板C保持静止.
(2)由动量守恒定律得:mv01-mv02=3mv
得v=
| 2 |
| 3 |
(3)A、B的加速度大小相等,aA=aB=μg=2m/s2
B先相对于C静止,运动时间t1=
| vB |
| aB |
此时A的速度,vA1=vA-aA′t1=2m/s
这段时间C一直保持静止状态,A、B的位移分别为:sA=vAt -
| 1 |
| 2 |
| t | 2 |
| 5 |
| 4 |
sB=
| 1 |
| 2 |
| 1 |
| 4 |
以后B相对于木板静止,A继续减速运动,木板的加速度:
ac=
| μmAg |
| mB+mC |
设此后A与木板的相对运动时间为t2,
vA1-aA′t2=act2
t2=
| 2 |
| 3 |
在t2时间内,A与木板相对运动距离△s=
| 2 |
| 3 |
木板的最小长度 s=s0+s1+s2+s3=2.37(m)
另一种方法:直接用动量守恒定律和能量转化方程.
由动量守恒定律得:mv01-mv02=3mv
得v=
| 2 |
| 3 |
当B相对地速度为0后,BC一起向左加速,直至三者速度相等.
当vB=0时,由动量守恒定律得:mv01-mv02=mv1+0
得:v1=2m/s
因为
. |
| vB |
| 1 |
| 2 |
. |
| vA |
| 5 |
| 2 |
所以s1=2 s2
由能量关系得:
| 1 |
| 2 |
| v | 2 01 |
| v | 2 02 |
| 1 |
| 2 |
| v | 2 1 |
得:s1=1.25(m),s2=0.25(m)
BC相对静止后,
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 |
s3=
| 2 |
| 3 |
L=s0+s1+s2+s3=2.37(m)
答:(1)在A、B同时运动的过程中,木板C保持静止
(2)若A、B最终不滑离木板,最后它们的共同速度为
| 2 |
| 3 |
(3)若要使A、B最终不滑离木板,木板C的长度至少为2.37(m)
点评:本题是相对运动的题目,要求同学们能正确分析物体的受力情况和运动情况,根据牛顿第二定律及运动学基本规律解题,难度较大.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图,有一半径为R=0.3m的光滑半圆形细管AB,将其固定在竖直墙面并使B端切线水平.一个可视为质点的质量为0.5Kg的小物体m由细管上端沿A点切线方向进入细管,从B点以速度VB=4.0m/s飞出后,恰好能从一倾角为θ=37°的倾斜传送带顶端C无碰撞的滑上传送带.已知传送带长度为L=2.75m(图中只画出了传送带的部分示意图),物体与传送带之间的动摩擦因数为u=0.50,(取sin37°=0.60,cos37°=0.80,g=10m/s2,不计空气阻力,不考虑半圆形管AB的内径).
如图,有一半径为R=0.3m的光滑半圆形细管AB,将其固定在竖直墙面并使B端切线水平.一个可视为质点的质量为0.5Kg的小物体m由细管上端沿A点切线方向进入细管,从B点以速度VB=4.0m/s飞出后,恰好能从一倾角为θ=37°的倾斜传送带顶端C无碰撞的滑上传送带.已知传送带长度为L=2.75m(图中只画出了传送带的部分示意图),物体与传送带之间的动摩擦因数为u=0.50,(取sin37°=0.60,cos37°=0.80,g=10m/s2,不计空气阻力,不考虑半圆形管AB的内径).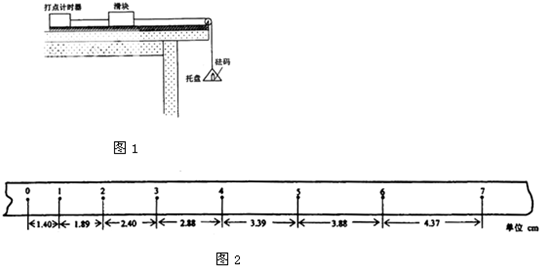
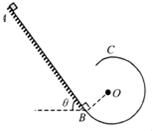 如图,是一段光滑的固定斜面,长度s=1m,与水平面 的倾角θ=530.另有一固定竖直放置的粗糙圆弧形轨道刚好在B点与斜面相切,圆弧形轨道半径R=0.3m,O点是圆弧轨道的 圆心.将一质量m=0.2kg的小物块从A点由静止释放,运动到 圆弧轨道最高点C点时,与轨道之间的弹力F=1N.重力加速度g=10m/s2,sin53°=0.8,cos53°=0.6,不计空气阻力.求:
如图,是一段光滑的固定斜面,长度s=1m,与水平面 的倾角θ=530.另有一固定竖直放置的粗糙圆弧形轨道刚好在B点与斜面相切,圆弧形轨道半径R=0.3m,O点是圆弧轨道的 圆心.将一质量m=0.2kg的小物块从A点由静止释放,运动到 圆弧轨道最高点C点时,与轨道之间的弹力F=1N.重力加速度g=10m/s2,sin53°=0.8,cos53°=0.6,不计空气阻力.求: