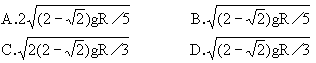题目内容
 如图,有一半径为R=0.3m的光滑半圆形细管AB,将其固定在竖直墙面并使B端切线水平.一个可视为质点的质量为0.5Kg的小物体m由细管上端沿A点切线方向进入细管,从B点以速度VB=4.0m/s飞出后,恰好能从一倾角为θ=37°的倾斜传送带顶端C无碰撞的滑上传送带.已知传送带长度为L=2.75m(图中只画出了传送带的部分示意图),物体与传送带之间的动摩擦因数为u=0.50,(取sin37°=0.60,cos37°=0.80,g=10m/s2,不计空气阻力,不考虑半圆形管AB的内径).
如图,有一半径为R=0.3m的光滑半圆形细管AB,将其固定在竖直墙面并使B端切线水平.一个可视为质点的质量为0.5Kg的小物体m由细管上端沿A点切线方向进入细管,从B点以速度VB=4.0m/s飞出后,恰好能从一倾角为θ=37°的倾斜传送带顶端C无碰撞的滑上传送带.已知传送带长度为L=2.75m(图中只画出了传送带的部分示意图),物体与传送带之间的动摩擦因数为u=0.50,(取sin37°=0.60,cos37°=0.80,g=10m/s2,不计空气阻力,不考虑半圆形管AB的内径).(1)求物体在A点时的速度大小及对轨道的压力大小和方向;
(2)若传送带以V1=2.5m/s顺时针匀速转动,求物体从C到底端的过程中,由于摩擦而产生的热量Q.
分析:(1)物体从A运动到B的过程中,只有重力做功,机械能守恒,已知高度为2R,物体在B点的速度,根据机械能守恒定律求出物体在A点时的速度.在A点,由重力和轨道的弹力的合力提供物体的向心力,由牛顿运动定律求解物体对轨道的压力.
(2)物体从B点滑出后做平抛运动,滑上传送带时,速度沿传送带方向,与水平方向的夹角等于θ,作出速度分解图,求出物体落到传送带顶端C时的速度大小.由于传送带顺时针匀速转动,物体滑上传送带后,受到的滑动摩擦力沿斜面向上,由于μmgcosθ<mgsinθ,物体向下做匀加速运动,根据牛顿第二定律求出加速度,由位移公式求出物体从C到底端的时间,并求解传送带相对于地运动的位移.物体摩擦而产生的热量Q=f?△x,物体与传送带相对位移△x是物体对地位移与传送带对地位移之和.
(2)物体从B点滑出后做平抛运动,滑上传送带时,速度沿传送带方向,与水平方向的夹角等于θ,作出速度分解图,求出物体落到传送带顶端C时的速度大小.由于传送带顺时针匀速转动,物体滑上传送带后,受到的滑动摩擦力沿斜面向上,由于μmgcosθ<mgsinθ,物体向下做匀加速运动,根据牛顿第二定律求出加速度,由位移公式求出物体从C到底端的时间,并求解传送带相对于地运动的位移.物体摩擦而产生的热量Q=f?△x,物体与传送带相对位移△x是物体对地位移与传送带对地位移之和.
解答:解:
(1)物体从A到B过程,根据机械能守恒定律得
mg?2R=
m
-
m
得:vA=2m/s
设物体在A点所受轨道作用力为FA,
则由mg+FA=m
,可得:FA=
N=1.67N;
由牛顿第三定律得:物体在A点时对轨道的压力大小为1.67N,方向为:竖直向上
(2)物体落到传送带顶端C时的速度大小为:
vC=
=5m/s
传送带顺时针匀速转动时,对物体施加的摩擦力沿传送带表面向上
则由牛顿第二定律得
mg(sinθ-μcosθ)=ma,
可得物体匀加速运动的加速度大小为:a=2m/s2
由L=vCt+
a1t2,得物体从C到底端的时间:t=0.5s
在此过程中,传送带相对地位移大小为s带=v1t
由于摩擦而产生的热量为Q=f?(L+s带)=μmgcosθ?(L+v1t)=8J
答:(1)物体在A点时的速度大小是2m/s,对轨道的压力大小为1.67N,方向为竖直向上;
(2)若传送带以V1=2.5m/s顺时针匀速转动,求物体从C到底端的过程中,由于摩擦而产生的热量Q=8J.
(1)物体从A到B过程,根据机械能守恒定律得
mg?2R=
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
| v | 2 A |
得:vA=2m/s
设物体在A点所受轨道作用力为FA,
则由mg+FA=m
| ||
| R |
| 5 |
| 3 |
由牛顿第三定律得:物体在A点时对轨道的压力大小为1.67N,方向为:竖直向上
(2)物体落到传送带顶端C时的速度大小为:
vC=
| vB |
| cosθ |
传送带顺时针匀速转动时,对物体施加的摩擦力沿传送带表面向上
则由牛顿第二定律得
mg(sinθ-μcosθ)=ma,
可得物体匀加速运动的加速度大小为:a=2m/s2
由L=vCt+
| 1 |
| 2 |
在此过程中,传送带相对地位移大小为s带=v1t
由于摩擦而产生的热量为Q=f?(L+s带)=μmgcosθ?(L+v1t)=8J
答:(1)物体在A点时的速度大小是2m/s,对轨道的压力大小为1.67N,方向为竖直向上;
(2)若传送带以V1=2.5m/s顺时针匀速转动,求物体从C到底端的过程中,由于摩擦而产生的热量Q=8J.
点评:本题文字较多,题目较长,但物理情景比较简单,按程序法进行分析,可以正确解答.对于摩擦生热要注意:热量等于摩擦力大小与相对位移大小的乘积.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
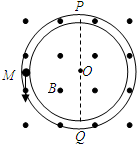 如图所示一半径为R=2.5m的内壁光滑绝缘的圆环竖直放置,环内有一质量为m=0.01kg、电荷量q=-0.2C的带电小球(可视为质点),在空间中存在竖直纸面向外的匀强磁场,磁感应强度为B=0.5T.图中虚线PQ为圆环竖直方向的一条直径.现让小球从与圆心O等高处的M点以某一初速度竖直向下开始运动,恰好能通过圆环的最高点P.求小球在最低点对圆环的压力大小及方向.
如图所示一半径为R=2.5m的内壁光滑绝缘的圆环竖直放置,环内有一质量为m=0.01kg、电荷量q=-0.2C的带电小球(可视为质点),在空间中存在竖直纸面向外的匀强磁场,磁感应强度为B=0.5T.图中虚线PQ为圆环竖直方向的一条直径.现让小球从与圆心O等高处的M点以某一初速度竖直向下开始运动,恰好能通过圆环的最高点P.求小球在最低点对圆环的压力大小及方向.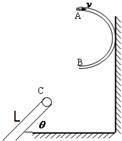
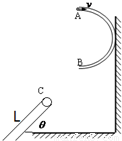
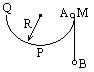 如图,有一半径为R的半圆形曲面MPQ,质量为2m的A球与质量为m的B球, 用轻质绳连接后挂在圆柱曲面边缘.现将A球从边缘M点由静止释放, 若不计一切摩擦,则A球沿圆柱曲面滑到最低点P时,其速度大小为
如图,有一半径为R的半圆形曲面MPQ,质量为2m的A球与质量为m的B球, 用轻质绳连接后挂在圆柱曲面边缘.现将A球从边缘M点由静止释放, 若不计一切摩擦,则A球沿圆柱曲面滑到最低点P时,其速度大小为