题目内容
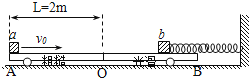
【题目】如图所示．在光滑的水平地面上停着一辆质量为m1=20Kg的小车A ， 有一质量为m2=15Kg的小木块C静止于小车A的右端，另有一辆质量为m3=25Kg的小车B以V0=3m/S的速度向右运动，与小车A发生碰撞，碰撞后连在一起运动（两车相碰时间极短）．假定车A足够长，木块与小车A的动摩擦因数为=0.2（g取10m/S2 ， 计算结果小数点后保留两位）．试求：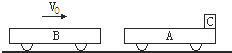
（1）碰撞结束瞬间小车A的速度大小
（2）木块在小车A上滑动的距离．
【答案】
（1）
A、B两车碰撞瞬间，设向右为正，由动量守恒定律得
m3V0=（m1+m3）V
解得V=1.67m/S
（2）
A、B两车以及木块为对象，由动量守恒定律得
m3V0=（m1+m3+m2）V共
由功能关系得
m2gS= 
（m1+m3）V2﹣ （m1+m3+m2）V共2
联立解得S=0.52m
【解析】（1）两车碰撞时系统的动量守恒，碰后两球的速度相等，根据动量守恒定律可求得A的速度；（2）将两车及物体视为一个系统，由动量守恒定律可求得碰后的速度；再由功能关系可求得物体在小车上滑行的距离．
【考点精析】利用动量守恒定律对题目进行判断即可得到答案，需要熟知动量守恒定律成立的条件：系统不受外力或系统所受外力的合力为零；系统所受的外力的合力虽不为零，但系统外力比内力小得多；系统所受外力的合力虽不为零，但在某个方向上的分量为零，则在该方向上系统的总动量的分量保持不变．
练习册系列答案
相关题目
