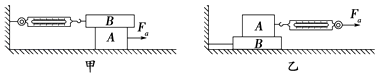
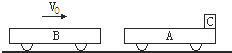
��Ŀ����
����Ŀ����ͼ��ʾ��ˮƽ��⻬�����ʵ����Ҷ˹̶������˨�����b �� С������M=3kg �� �ֲڲ���AO��L=2m �� ��Ħ��������=0.3��OB���ֹ⻬����һС���a �� ���ڳ�������ˣ��ͳ�һ����v0=4m/S���ٶ����������˶�����ײ���̶������˲���ٶȱ�Ϊ�㣬�����뵲��ճ������֪��OB���ֵij��ȴ��ڵ��ɵ���Ȼ���ȣ�����ʼ�մ��ڵ������ڣ�A��B�������Ϊ�ʵ�������Ϊm=1kg �� ��ײʱ�伫���Ҳ�ճ��������һ�������˶�����ȡg=10m/S2����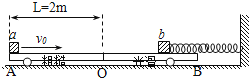
��1�����a��b��ǰ���ٶȴ�С��
��2�����ɾ��е���������ܣ�
��3�������a���С����ֹʱ��С���ϵ�λ�þ�O���Զ��
��4�������a���С����ֹʱС���Ҷ�B�൲���Զ��
���𰸡�
��1��
�����a���ɶ��ܶ����ã� ![]() ��
��
�������ݽ��a��b��ǰ�ٶȣ�v1=2m/S
��2��
A��B��ײ����ϵͳ�����غ㣬��a�ij��ٶȷ���Ϊ������
�ɶ����غ㶨�ɵã�mv1=2mv2���������ݽ�ã�v2=1m/S��
�������غ㶨�ɵã����ɵ���������ܣ�EP= ![]() 2mv22���������ݽ�ã�EP=1J
2mv22���������ݽ�ã�EP=1J
��3��
�����ɻָ���ԭ��ʱ�������룬a��v2=1m/S��С�������������복ͬ��ʱ��������Ϊ�������ɶ����غ㶨�ɵã�
mv2=��M+m��v3���������ݽ�ã�v3=0.25m/S��
�������غ�ã� ![]()
��û���a�복��Ծ�ֹʱ��O����룺x=0.125m
��4��
��С�����ɶ��ܶ����ã� ![]() ��
��
�������ݽ�ã�ͬ��ʱ��B�˾൲��ľ��룺 ![]()
����������1���ɶ��ܶ���������������ٶȣ���2���ɶ����غ㶨���������غ㶨�������������ܣ���3���ɶ����غ㶨���������غ㶨�ɿ���������룮��4���ɶ��ܶ�������������룮
�����㾫�������ڱ��⿼��Ķ����غ㶨�ɣ���Ҫ�˽���غ㶨�ɳ�����������ϵͳ����������ϵͳ���������ĺ���Ϊ�㣻ϵͳ���ܵ������ĺ����䲻Ϊ�㣬��ϵͳ����������С�öࣻϵͳ���������ĺ����䲻Ϊ�㣬����ij�������ϵķ���Ϊ�㣬���ڸ÷�����ϵͳ���ܶ����ķ������ֲ�����ܵó���ȷ�𰸣�