��Ŀ����
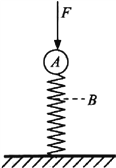
����Ŀ����ͼ��ʾ���ֲڻ��ι���������⻬��Բ��������β�͵�S�ι�����⻬��Բ����뾶ΪR�������⻬��Բ������Ӵ�CD֮�����к�С��϶���պ��ܹ�ʹС��ͨ����CD֮�����ɺ��ԣ��ֲڻ��ι����ߵ�A��ˮƽ����B��֮��ĸ߶�Ϊh����A�㾲ֹ�ͷ�һ������Ϊ�ʵ��С��С������β�͵�S�ι���˶����E��ˮƽ�ɳ����䵽ˮƽ�����ϣ���㵽��E����ͬһ��ֱ����B��ľ���Ϊs����֪С������m�����ƿ�����������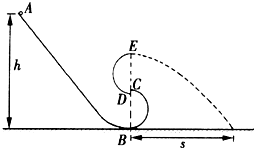
��1��С���E��ˮƽ�ɳ�ʱ���ٶȴ�С��
��2��С���˶�����Բ�����B��ʱ�Թ����ѹ����
��3��С������β��S�ι���˶�ʱ�˷�Ħ�������Ĺ���
���𰸡�
��1���⣺С���E��ˮƽ�ɳ���ƽ���˶�����С���E��ˮƽ�ɳ�ʱ���ٶȴ�СΪvE����ƽ���˶����ɵã�
s=vEt
![]()
������ã� ![]()
��С���E��ˮƽ�ɳ�ʱ���ٶȴ�СΪ ![]() ��
��
��2��С���B���˶���E��Ĺ��̣���е���غ㣬���ݻ�е���غ㶨�ɵã�
![]()
��ã� ![]()
��B�㣬����ţ�ٵڶ����ɵã� ![]()
�ã� ![]()
��ţ�ٵ������ɿ�֪С���˶���B��ʱ�Թ����ѹ��Ϊ ![]() ��������ֱ����
��������ֱ����
��С���˶�����Բ�����B��ʱ�Թ����ѹ����СΪ ![]() ��������ֱ���£�
��������ֱ���£�
��3����С������β�͵�S�ι���˶�ʱ�˷�Ħ�������Ĺ�ΪW����
![]()
�� ![]()
��С������β��S�ι���˶�ʱ�˷�Ħ�������Ĺ�Ϊ ![]() ��
��
��������(1)С���E��ˮƽ�ɳ�����ƽ���˶����г���ֱ��ˮƽ����λ�ƹ�ʽ����ֱ�߶Ⱦ����˶�ʱ�䣬ˮƽλ�Ƴ���ʱ��С���E��ˮƽ�ɳ�ʱ���ٶȡ�
(2)С���˶�����Բ�����B��ʱ���������ṩ����������е���غ㶨�����С��B��ʱ�Ķ��ܣ��ɽ⡣
(3)С������β�͵�S�ι���˶�ʱ��ֻ��Ħ�������������������ݶ��ܶ����������С������β�͵�S�ι���˶�ʱ�˷�Ħ�������Ĺ���

 ��ʦ�㾦�ִʾ��ƪϵ�д�
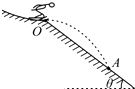
��ʦ�㾦�ִʾ��ƪϵ�д�����Ŀ����ͼ��ʾ������ӹ⻬б���ϵ�A���ɾ�ֹ��ʼ�»�������B������ˮƽ�棨�辭��B��ǰ���ٶȴ�С���䣩�����ͣ��C�㡣ÿ��0.2sͨ���ٶȴ��������������˲ʱ�ٶȡ��±������˲��ֲ������ݡ���������б��֮�䡢������ˮƽ��֮��Ķ�Ħ����������ͬ����

| 0.0 | 0.2 | 0.4 | ���� | 0.8 | 1.0 | ���� |
| 0.00 | 0.80 | 1.60 | ���� | 1.25 | 0.75 | ���� |
��1��������б�����˶��ļ��ٶȴ�Сa��
��2��������б�����˶���ʱ��t��
��3��б����ˮƽ��֮��ļн�![]() ��
��