题目内容
【题目】如图所示,在空间有一坐标系![]() 直线
直线![]() 与
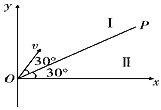
与![]() 轴正方向的夹角为30°,第一象限内有两个方向都垂直纸面向外的匀强磁场区域Ⅰ和Ⅱ,直线
轴正方向的夹角为30°,第一象限内有两个方向都垂直纸面向外的匀强磁场区域Ⅰ和Ⅱ,直线![]() 是他们的边界,
是他们的边界,![]() 上方区域Ⅰ中磁场的磁感应强度为
上方区域Ⅰ中磁场的磁感应强度为![]() 一质量为
一质量为![]() 电荷量为
电荷量为![]() 的质子(不计重力)以速度
的质子(不计重力)以速度![]() 从
从![]() 点沿与
点沿与![]() 成30°角的方向垂直磁场进入区域Ⅰ,质子先后通过磁场区域和Ⅱ后,恰好垂直打在
成30°角的方向垂直磁场进入区域Ⅰ,质子先后通过磁场区域和Ⅱ后,恰好垂直打在![]() 轴上的Q点(图中未画出),则
轴上的Q点(图中未画出),则
A. 质子在区域Ⅰ中运动的时间为![]()
B. 质子在区域Ⅰ中运动的时间为![]()
C. 质子在区域Ⅱ中运动的时间为![]()
D. 质子在区域Ⅱ中运动的时间为![]()
【答案】BD
【解析】
设质子在磁场I和II中做圆周运动的轨道半径分别为r1和r2,区域II中磁感应强度为B′,由牛顿第二定律得:qvB=m![]() ①;qvB′=m
①;qvB′=m![]() ②;粒子在两区域运动的轨迹如图所示,由带电粒子才磁场中运动的对称性和几何关系可知,质子从A点出磁场I时的速度方向与OP的夹角为30°,故质子在磁场I中轨迹的圆心角为:θ=60°,如图所示:
②;粒子在两区域运动的轨迹如图所示,由带电粒子才磁场中运动的对称性和几何关系可知,质子从A点出磁场I时的速度方向与OP的夹角为30°,故质子在磁场I中轨迹的圆心角为:θ=60°,如图所示:
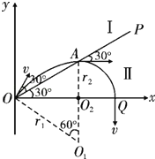
则△O1OA为等边三角形,有:OA=r1 ③,在区域II中,质子运动![]() 圆周,O2是粒子在区域II中做圆周运动的圆心,r2=OAsin30°④,由①②③④解得区域II中磁感应强度为:B′=2B ⑤,质子在Ⅰ区运动轨迹对应的圆心角:φ=60°,在Ⅱ区运动轨迹对应的圆心角为:φ′=90°,质子在Ⅰ区的运动周期:T1
圆周,O2是粒子在区域II中做圆周运动的圆心,r2=OAsin30°④,由①②③④解得区域II中磁感应强度为:B′=2B ⑤,质子在Ⅰ区运动轨迹对应的圆心角:φ=60°,在Ⅱ区运动轨迹对应的圆心角为:φ′=90°,质子在Ⅰ区的运动周期:T1![]() ,运动时间t1
,运动时间t1![]() ,故A错误,B正确;质子在Ⅱ区运动的周期:T2
,故A错误,B正确;质子在Ⅱ区运动的周期:T2![]() ,运动时间t2
,运动时间t2![]() ,故C错误,D正确;
,故C错误,D正确;

练习册系列答案
相关题目