��Ŀ����
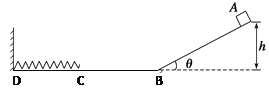
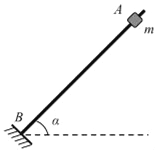
����Ŀ����ͼ��ʾ��ֱ��AB��ˮƽ������ǹ̶����ڸ�����һ����Ϊm��С���飬���뻬��Ķ�Ħ������������ͬ���˵�B�㴦��һ����洹ֱ�ĵ��Ե��壮�����뵲����ײ��ԭ���ʷ��أ��ֽ���������A���ɾ�ֹ�ͷţ������뵲���һ����ײ�������ĸ߶�Ϊԭ����k��k��1����������֪���ǡ�����m������ϵ��k���������ٶ�g������˵������ȷ���ǣ�������
A. ������������ڸ����˶�����·��
B. ������������n���뵲����ײǰ����������˲ʱ����P
C. ������������»����ϻ����̼��ٶȵĴ�С
D. ȡ��B���ˮƽ��Ϊ�������棬������жϻ����A�»���B�Ĺ����У��������ܵ��ڶ��ܵ�λ����AB�е���·�
���𰸡�CD
����������AB��ΪL�������뵲���һ����ײ�������ĸ߶�Ϊԭ����k��k��1�����������ϵľ���ΪkL�����������̣����ö��ܶ����ã�mgsin����1��k��L����mgcos����L+kL��=0
�ã���=![]() �����Կ��������Ħ�������̣�
�����Կ��������Ħ�������̣�
�����˶��Ĺ�������������ת��Ϊ���ܣ�����mgcos��S��=mgsin��L
����AB֮��ľ�����δ֪�ģ����Բ�����������ڸ����˶�����·�̣���A����
����AB֮��ľ�����δ֪�ģ����ԣ�Ҳ������������n���뵲����ײǰ���ٶȣ����Բ����������������˲ʱ����P����B������
����ţ�ٵڶ����ɵ��»������У�mgsin������mgcos��=ma1
�ϻ������У�mgsin��+��mgcos��=ma2��
��ã�a1=mgsin������gcos����a2=gsin��+��gcos��
���Կ���û����»����ϻ����̼��ٶȵĴ�Сa1��a2����C��ȷ��
�������»����Ĺ����У���������������Ħ������������ȡ��B���ˮƽ��Ϊ�������棬�����黬��AB���е㴦ʱ��һ�����������ת��Ϊ����Ķ��ܺͲ��������ܣ����Ե����黬��AB���е㴦ʱ������Ķ���С�ڻ�����������ܣ�����ȡ��B���ˮƽ��Ϊ�������棬������жϻ����A�»���B�Ĺ����У��������ܵ��ڶ��ܵ�λ����AB�е���·�����D��ȷ����ѡCD.