题目内容
【题目】一轻质弹簧水平放置,一端固定在A点,另一端与质量为m的小物块P接触但不连接.AB是水平轨道,质量也为m的小物块Q静止在B点,B端与半径为l的光滑半圆轨道BCD相切,半圆的直径BD竖直,如图所示.物块P与AB间的动摩擦因数μ=0.5.初始时PB间距为4l,弹簧处于压缩状态.释放P,P开始运动,脱离弹簧后在B点与Q碰撞后粘在一起沿轨道运动,恰能经过最高点D,己知重力加速度g,求:
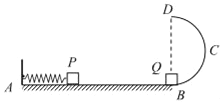
(1)粘合体在B点的速度.
(2)初始时弹簧的弹性势能.
【答案】(1)![]() .(2)12mgl.
.(2)12mgl.
【解析】(1)物块P恰好能够到达D点时,由重力提供向心力,由牛顿第二定律有:
mg=m![]()
可得:vD=![]()
从B到D,由机械能守恒定律得:
2mgl+![]() mvD2=
mvD2=![]() mvB2
mvB2
得: ![]()
(2)P与Q碰撞的过程时间短,水平方向的动量守恒,选取向右为正方向,设碰撞前P的速度为v,则:mv=2mvB
P从开始释放到到达Q的过程中,弹簧的弹力对P做正功,地面的摩擦力对P做负功,由功能关系得: ![]()
联立得:EP=12mgl

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目