题目内容
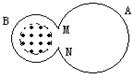如图所示，用同种材料制成的粗细相同的金属圆环A和B，电阻RA=2RB；虚线框内有随时间均匀变化的磁场；此磁场在圆环B内时，M、N两点间电势差大小为1.8V，则将该磁场放入A圆环内时，M、N两点间电势差大小为（ ）分析：A环与B环的半径之比为2：1，故周长之比为2：1，根据电阻定律R=ρ
，电阻之比为2：1；根据法拉第电磁感应定律公式E=n
得到两次电动势的大小关系，然后结合闭合电路欧姆定律分析即可．
| L |
| S |
| △Φ |
| △t |
解答：解：A环与B环的半径之比为2：1，故周长之比为2：1，根据电阻定律R=ρ
，电阻之比为2：1；
M、N两点间电势差大小为路端电压，为：U=
E；
两次磁通量相等，故根据法拉第电磁感应定律公式E=n
得到两次电动势的大小相等；
故两次的路段电压之比为U1：U2=RA：RB=2：1，故U2=
U1=0.9V；
故选C．
| L |
| S |
M、N两点间电势差大小为路端电压，为：U=
| R外 |
| R外+R内 |
两次磁通量相等，故根据法拉第电磁感应定律公式E=n
| △Φ |
| △t |
故两次的路段电压之比为U1：U2=RA：RB=2：1，故U2=
| 1 |
| 2 |
故选C．
点评：本题关键是理清电路结构，然后根据闭合电路欧姆定律、电阻定律和法拉第电磁感应定律列式分析，不难．
练习册系列答案
名校课堂系列答案
相关题目
如图所示，用同种材料制成一轨道，AB段为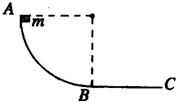
如图所示，用同种材料制成一个竖直平面内的轨道，AB段为
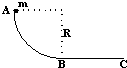如图所示，用同种材料制成的一个轨道，AB段为
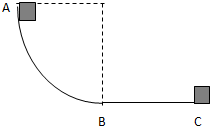如图所示，用同种材料制成的一个轨道ABC，AB段为四分之一圆弧，半径为R=2m，BC段为水平放置的轨道．一个物块质量为m=2kg，与轨道的动摩擦因数为μ=0.25，它由轨道顶端A从静止开始下滑，恰好运动到C端停止，测得物块滑至底端B点的速度为5m/s，求：（g取10m/s2）
如图所示，用同种材料制成倾角37°的斜面（足够长）和长水平面，斜面和水平面用长度不计的光滑圆弧连接，一小物块以水平初速度υ0=2.0m/s向右运动，经过0.4s后小物块恰停在斜面底端．（g=10m/s2，sin37°=0.6，cos37°=0.8）