题目内容
 如图所示,用同种材料制成一轨道,AB段为
如图所示,用同种材料制成一轨道,AB段为| 1 |
| 4 |
分析:BC段摩擦力可以求出,由做的公式可求得BC段克服摩擦力所做的功; 对全程由动能定理可求得AB段克服摩擦力所做的功.
解答:解:BC段物体受摩擦力f=μmg,位移为R,故BC段摩擦力对物体做功W=-fR=-μmgR;
即物体克服摩擦力做功为μmgR;对全程由动能定理可知,mgR+W1+W=0,
解得W1=μmgR-mgR,故AB段克服摩擦力做功为mgR(1-μ),故B正确.
故选:B.
即物体克服摩擦力做功为μmgR;对全程由动能定理可知,mgR+W1+W=0,
解得W1=μmgR-mgR,故AB段克服摩擦力做功为mgR(1-μ),故B正确.
故选:B.
点评:AB段的摩擦力为变力,故可以由动能定理求解; 而BC段为恒力,可以直接由功的公式求解; 同时本题需要注意阻力做功与克服阻力做功的关系.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
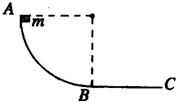 如图所示,用同种材料制成一个竖直平面内的轨道,AB段为
如图所示,用同种材料制成一个竖直平面内的轨道,AB段为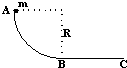 如图所示,用同种材料制成的一个轨道,AB段为
如图所示,用同种材料制成的一个轨道,AB段为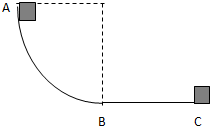 如图所示,用同种材料制成的一个轨道ABC,AB段为四分之一圆弧,半径为R=2m,BC段为水平放置的轨道.一个物块质量为m=2kg,与轨道的动摩擦因数为μ=0.25,它由轨道顶端A从静止开始下滑,恰好运动到C端停止,测得物块滑至底端B点的速度为5m/s,求:(g取10m/s2)
如图所示,用同种材料制成的一个轨道ABC,AB段为四分之一圆弧,半径为R=2m,BC段为水平放置的轨道.一个物块质量为m=2kg,与轨道的动摩擦因数为μ=0.25,它由轨道顶端A从静止开始下滑,恰好运动到C端停止,测得物块滑至底端B点的速度为5m/s,求:(g取10m/s2) 如图所示,用同种材料制成倾角37°的斜面(足够长)和长水平面,斜面和水平面用长度不计的光滑圆弧连接,一小物块以水平初速度υ0=2.0m/s向右运动,经过0.4s后小物块恰停在斜面底端.(g=10m/s2,sin37°=0.6,cos37°=0.8)
如图所示,用同种材料制成倾角37°的斜面(足够长)和长水平面,斜面和水平面用长度不计的光滑圆弧连接,一小物块以水平初速度υ0=2.0m/s向右运动,经过0.4s后小物块恰停在斜面底端.(g=10m/s2,sin37°=0.6,cos37°=0.8)