题目内容
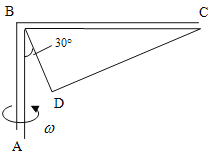
【题目】如图所示,直角架ABC的直角边AB在竖直方向上,B点和C点各系一细绳,两绳共吊着一质量为1kg的小球于D点,且BD⊥CD,∠ABD=30°,BD=40cm。当直角架以AB为轴,以10rad/s的角速度匀速转动时,绳BD和CD的拉力各为多少?(g取10m/s2)
【答案】40N,0
【解析】
球随着杆一起做圆周运动,先假设绳CD没有力的作用,来判断球的运动状态,根据球的运动的状态来分析绳BC是否被拉直,在进一步分析绳子的拉力的大小。
设角架以ω0转动时,TCD=0,其中r=|BD|sin30°=0.2m
此时对小球分析,由牛顿第二定律有:mgtan30°=mrω02
解得:![]()
所以当ω=10rad/s时,CD绳无拉力
设此时BD与AB夹角为θ,则有![]()
而![]()
联立可得:![]() ,TCD=0
,TCD=0

练习册系列答案
相关题目