题目内容
如图所示,质量为m的导体棒曲垂直放在光滑足够长的U形导轨的底端,导轨宽度和棒长相等且接触良好,导轨平面与水平面成 角,整个装置处在与导轨平面垂直的匀强磁场中.现给导体棒沿导轨向上的初速度v0,经时间t0导体棒到达最高点,然后开始返回,到达底端前已经做匀速运动,速度大小为
角,整个装置处在与导轨平面垂直的匀强磁场中.现给导体棒沿导轨向上的初速度v0,经时间t0导体棒到达最高点,然后开始返回,到达底端前已经做匀速运动,速度大小为 .已知导体棒的电阻为R,其余电阻不计,重力加速度为g,忽略电路中感应电流之间的相互作用.求:
.已知导体棒的电阻为R,其余电阻不计,重力加速度为g,忽略电路中感应电流之间的相互作用.求:

小题1:导体棒从开始运动到返回底端的过程中,回路中产生的电能;
小题2:导体棒在底端开始运动时的加速度大小;
小题3:导体棒上升的最大高度.
 角,整个装置处在与导轨平面垂直的匀强磁场中.现给导体棒沿导轨向上的初速度v0,经时间t0导体棒到达最高点,然后开始返回,到达底端前已经做匀速运动,速度大小为
角,整个装置处在与导轨平面垂直的匀强磁场中.现给导体棒沿导轨向上的初速度v0,经时间t0导体棒到达最高点,然后开始返回,到达底端前已经做匀速运动,速度大小为 .已知导体棒的电阻为R,其余电阻不计,重力加速度为g,忽略电路中感应电流之间的相互作用.求:
.已知导体棒的电阻为R,其余电阻不计,重力加速度为g,忽略电路中感应电流之间的相互作用.求:
小题1:导体棒从开始运动到返回底端的过程中,回路中产生的电能;
小题2:导体棒在底端开始运动时的加速度大小;
小题3:导体棒上升的最大高度.
小题1:
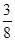 mv02
mv02小题2:a1 = 3gsinθ
小题3:(v02-gv0t0sinθ)/2g
⑴据能量守恒,得 △E = mv02 - m(
m( )2=
)2= 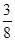 mv02
mv02
⑵在底端,设棒上电流为I,加速度为a,由牛顿第二定律,则:)
(mgsinθ+BIL)=ma1
由欧姆定律,得I= E=BLv0
由上述三式,得a1 =" " gsinθ +
∵棒到达底端前已经做匀速运动∴mgsinθ=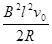
代入,得a1 = 3gsinθ
(3)选沿斜面向上为正方向,上升过程中的加速度,上升到最高点的路程为S,
a = -(gsinθ + )
取一极短时间△t,速度微小变化为△v,由△v = a△t,得
△ v = -( gsinθ△t+B2L2v△t/mR)
其中,v△t = △s
在上升的全过程中
∑△v = -(gsinθ∑△t+B2L2∑△s/mR)
即 0-v0= -(t0gsinθ+B2L2S/mR)
∵H="S·sinθ " 且mgsinθ=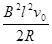
∴ H =(v02-gv0t0sinθ)/2g
 m(
m( )2=
)2= 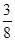 mv02
mv02 ⑵在底端,设棒上电流为I,加速度为a,由牛顿第二定律,则:)
(mgsinθ+BIL)=ma1
由欧姆定律,得I= E=BLv0
由上述三式,得a1 =" " gsinθ +
∵棒到达底端前已经做匀速运动∴mgsinθ=
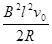
代入,得a1 = 3gsinθ
(3)选沿斜面向上为正方向,上升过程中的加速度,上升到最高点的路程为S,
a = -(gsinθ + )
取一极短时间△t,速度微小变化为△v,由△v = a△t,得
△ v = -( gsinθ△t+B2L2v△t/mR)
其中,v△t = △s
在上升的全过程中
∑△v = -(gsinθ∑△t+B2L2∑△s/mR)
即 0-v0= -(t0gsinθ+B2L2S/mR)
∵H="S·sinθ " 且mgsinθ=
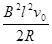
∴ H =(v02-gv0t0sinθ)/2g

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目


 穿过磁场Ⅰ后进入右边磁场Ⅱ并按某一路径再返回到磁场Ⅰ的边界MN上的某一点b(图中末画出),(途中虚线为磁场区域的分界面)求:
穿过磁场Ⅰ后进入右边磁场Ⅱ并按某一路径再返回到磁场Ⅰ的边界MN上的某一点b(图中末画出),(途中虚线为磁场区域的分界面)求:


 10-6 C的点电荷从无穷远移至电场中某点,电场力做功为4
10-6 C的点电荷从无穷远移至电场中某点,电场力做功为4 4×10-10N/C的带正电粒子从x轴上的A点以初速度v0=2×107m/s垂直x轴射入电场,OA=0.2m,不计重力。求:
4×10-10N/C的带正电粒子从x轴上的A点以初速度v0=2×107m/s垂直x轴射入电场,OA=0.2m,不计重力。求:
 的匀强磁场;在第三象限存在沿y轴正向的匀强电场,一质量为m带电量为+q的带电粒子从电场中的坐标为(-2h,
的匀强磁场;在第三象限存在沿y轴正向的匀强电场,一质量为m带电量为+q的带电粒子从电场中的坐标为(-2h, )点以速度
)点以速度 水平向右射出,经过原点O处射入区域I后垂直MN射入区域Ⅱ,(粒子的重力忽略不计)求:
水平向右射出,经过原点O处射入区域I后垂直MN射入区域Ⅱ,(粒子的重力忽略不计)求: