题目内容
【题目】如图所示，一束电子（电量为e）以速度v0垂直射入磁感应强度为B，宽为d的匀强磁场中，穿出磁场时速度方向与电子原来入射方向的夹角为30°，则电子的质量是多少？穿过磁场的时间是多少？
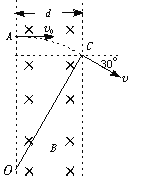
【答案】解析：电子在磁场中运动，只受洛伦兹力作用，故其轨迹是圆弧一部分，又因为f⊥v，故圆心在电子穿入和穿出磁场时受到洛伦兹力指向的交点上，如图16－60中的O点．由几何知识可知：AB间的圆心角θ＝30°，OB为半径．
r＝d/sin30°＝2d，又由r＝mv/Be得m＝2dBe/v．
由于AB圆心角是30°，故穿透时间t＝T/12＝πd/3v．
点拨：带电粒子的匀速圆周运动的求解关键是画出匀速圆周运动的轨迹，利用几何知识找出圆心及相应的半径，从而找到圆弧所对应的圆心角
【解析】试题分析：
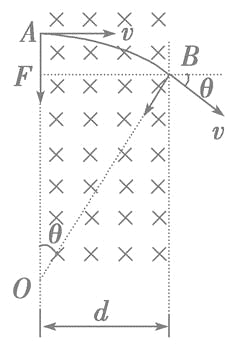
电子在匀强磁场中运动时，只受洛伦兹力作用，故其轨道是圆弧的一部分．又因洛伦兹力与速度v垂直，故圆心应在电子穿入和穿出时洛伦兹力延长线的交点上．从图中可以看出，AB弧所对的圆心角θ＝30°＝
，OB即为半径r
由几何关系可得：r＝
＝2d
由牛顿第二定律得：qvB＝
解得：m＝
＝
带电粒子通过AB弧所用的时间，即穿过磁场的时间为：t＝
T＝
×
＝
＝
.
练习册系列答案
相关题目
