题目内容
1.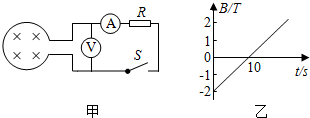 如图所示,单匝圆形线框中磁场正均匀变化,其磁感应强度随时间的变化关系已经在乙图标出,已知圆形线框面积为0.2m2,内阻r=1Ω,定值电阻R=1Ω,电表均为理想电表,其余电阻不计,以垂直纸面向外为磁感应强度正方形,则以下判断正确的是( )
如图所示,单匝圆形线框中磁场正均匀变化,其磁感应强度随时间的变化关系已经在乙图标出,已知圆形线框面积为0.2m2,内阻r=1Ω,定值电阻R=1Ω,电表均为理想电表,其余电阻不计,以垂直纸面向外为磁感应强度正方形,则以下判断正确的是( )| A. | 圆形线框中感应电流方向始终为逆时针 | |
| B. | 线框始终有扩张的趋势 | |
| C. | 电压表示数为1V | |
| D. | 电流表示数为0.02A |
分析 由楞次定律可以判断出感应电流方向、判断出线圈的变化趋势;
应用法拉第电磁感应定律可以求出感应电动势,然后应用欧姆定律可以求出电流表与电压表示数.
解答 解:A、由图乙所示图象可知,磁感应强度先减小后反向增大,由楞次定律可知,感应电流始终沿顺时针方向,故A错误;
B、在0-10s内磁感应强度减小,穿过线圈的磁通量减小,由楞次定律可知,线圈有扩张的趋势,在10s后穿过线圈的磁通量增加,由楞次定律可知,线圈有收缩的趋势,故B错误;
C、由法拉第电磁感应定律可知,感应电动势:E=$\frac{△Φ}{△t}$=$\frac{△B}{△t}$S=$\frac{0-(-2)}{10}$×0.2=0.04V,感应电流:I=$\frac{E}{R+r}$=$\frac{0.04}{1+1}$=0.02A,电压表示数:U=IR=0.02×1=0.02V,故C错误,D正确;
故选:D.
点评 考查楞次定律来判定感应电流方向,由法拉第电磁感应定律来求出感应电动势大小.当然本题还可求出电路的电流大小,及电阻消耗的功率.同时磁通量变化的线圈相当于电源.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
9.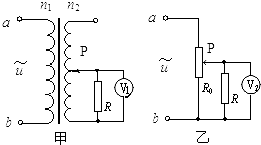 在图甲中,理想变压器的原、副线圈匝数之比n1:n2=1:3,滑片P置于副线圈的中点.在图乙中,滑动变阻器最大阻值R0=6Ω,滑动触头P置于R0的中央.两电路的输入端都接交流u=20$\sqrt{2}$sin100πt(V)的正弦交流电,输出端各接一个阻值R=6Ω的定值电阻和理想交流电压表.两电压表的读数U1、U2分别为( )
在图甲中,理想变压器的原、副线圈匝数之比n1:n2=1:3,滑片P置于副线圈的中点.在图乙中,滑动变阻器最大阻值R0=6Ω,滑动触头P置于R0的中央.两电路的输入端都接交流u=20$\sqrt{2}$sin100πt(V)的正弦交流电,输出端各接一个阻值R=6Ω的定值电阻和理想交流电压表.两电压表的读数U1、U2分别为( )
 在图甲中,理想变压器的原、副线圈匝数之比n1:n2=1:3,滑片P置于副线圈的中点.在图乙中,滑动变阻器最大阻值R0=6Ω,滑动触头P置于R0的中央.两电路的输入端都接交流u=20$\sqrt{2}$sin100πt(V)的正弦交流电,输出端各接一个阻值R=6Ω的定值电阻和理想交流电压表.两电压表的读数U1、U2分别为( )
在图甲中,理想变压器的原、副线圈匝数之比n1:n2=1:3,滑片P置于副线圈的中点.在图乙中,滑动变阻器最大阻值R0=6Ω,滑动触头P置于R0的中央.两电路的输入端都接交流u=20$\sqrt{2}$sin100πt(V)的正弦交流电,输出端各接一个阻值R=6Ω的定值电阻和理想交流电压表.两电压表的读数U1、U2分别为( )| A. | U1=30V,U2=8V | B. | U1=30V,U2=10V | C. | U1=60V,U2=8V | D. | U1=60V,U2=10V |
16.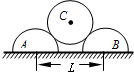 如图所示,两个截面半径均为r、质量均为m的半圆柱体A、B放在粗糙水平面上,A、B截面圆心间的距离为L.在A、B上放一个截面半径为r、质量为2m的光滑圆柱体C,A、B、C始终都处于静止状态,则( )
如图所示,两个截面半径均为r、质量均为m的半圆柱体A、B放在粗糙水平面上,A、B截面圆心间的距离为L.在A、B上放一个截面半径为r、质量为2m的光滑圆柱体C,A、B、C始终都处于静止状态,则( )
 如图所示,两个截面半径均为r、质量均为m的半圆柱体A、B放在粗糙水平面上,A、B截面圆心间的距离为L.在A、B上放一个截面半径为r、质量为2m的光滑圆柱体C,A、B、C始终都处于静止状态,则( )
如图所示,两个截面半径均为r、质量均为m的半圆柱体A、B放在粗糙水平面上,A、B截面圆心间的距离为L.在A、B上放一个截面半径为r、质量为2m的光滑圆柱体C,A、B、C始终都处于静止状态,则( )| A. | B对地面的压力大小为3mg | |
| B. | 地面对A的作用力沿AC圆心连线方向 | |
| C. | L越小,A、C间的弹力越小 | |
| D. | L越小,地面对A、B的摩擦力越大 |
10. 如图(a),一物块在t=0时刻滑上一固定斜面,其运动的v-t图线如图(b)所示,若重力加速度及图中的v0,v1,t1均为已知量,则可求出( )
如图(a),一物块在t=0时刻滑上一固定斜面,其运动的v-t图线如图(b)所示,若重力加速度及图中的v0,v1,t1均为已知量,则可求出( )
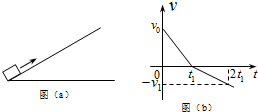 如图(a),一物块在t=0时刻滑上一固定斜面,其运动的v-t图线如图(b)所示,若重力加速度及图中的v0,v1,t1均为已知量,则可求出( )
如图(a),一物块在t=0时刻滑上一固定斜面,其运动的v-t图线如图(b)所示,若重力加速度及图中的v0,v1,t1均为已知量,则可求出( )| A. | 斜面的倾角 | B. | 物块的质量 | ||
| C. | 物块与斜面间的动摩擦因数 | D. | 物块沿斜面向上滑行的最大高度 |
 某同学想描绘一只标称为“2.5V,1.5W”的小灯泡的伏安特性曲线,实验室提供下列器材:
某同学想描绘一只标称为“2.5V,1.5W”的小灯泡的伏安特性曲线,实验室提供下列器材: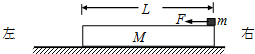 如图所示,质量为M0=4kg的木板静止在光滑的水平面上,在木板的右端放置一个质量m=1kg大小可以忽略的铁块,铁块与木板之间的摩擦因数μ=0.4,在铁块上加一个水平向左的恒力F=8N,铁块在长L=6m的木板上滑动.取g=10m/s2.求:
如图所示,质量为M0=4kg的木板静止在光滑的水平面上,在木板的右端放置一个质量m=1kg大小可以忽略的铁块,铁块与木板之间的摩擦因数μ=0.4,在铁块上加一个水平向左的恒力F=8N,铁块在长L=6m的木板上滑动.取g=10m/s2.求: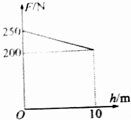 用质量为5kg的均匀铁索,从10m深的井中吊起一质量为20kg的物体,其过程中人的拉力随物体上升的高度变化如图所示,在这个过程中人至少要做多少功?(g取10m/s2)
用质量为5kg的均匀铁索,从10m深的井中吊起一质量为20kg的物体,其过程中人的拉力随物体上升的高度变化如图所示,在这个过程中人至少要做多少功?(g取10m/s2)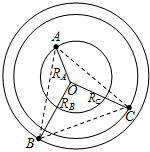 由三颗星体构成的系统,忽略其它星体对它们的作用,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O在三角形所在的平面内做相同角速度的圆周运动(图示为A、B、C三颗星体质量不相同时的一般情况).若A星体质量为2m,B、C两星体的质量均为m,三角形的边长为a,求:
由三颗星体构成的系统,忽略其它星体对它们的作用,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O在三角形所在的平面内做相同角速度的圆周运动(图示为A、B、C三颗星体质量不相同时的一般情况).若A星体质量为2m,B、C两星体的质量均为m,三角形的边长为a,求: