题目内容
abcd是质量为m,长和宽分别为b和l的矩形金属线框,有静止沿两条平行光滑的倾斜轨道下滑,轨道平面与水平面成θ角。efmn为一矩形磁场区域,磁感应强度为B,方向竖直向上。已知da=an=ne=b,线框的cd边刚要离开磁区时的瞬时速度为v,整个线框的电阻为R,试用题中给出的物理量(m、b、l、B、θ、v、R)表述下列物理量。
(1)ab刚进入磁区时产生的感应电动势;
(2)此时线框的加速度;
(3)线框下滑中共产生的热量。
(1) (2)
(2) (3)
(3)
解析试题分析:(1)设ab边进入磁区时的速度为v,由机械能守恒定律可得: 可得:
可得:
所以,ab刚进入磁区时产生的感应电动势
(2)当ab边刚进入磁区时,受到的安培力为:
由牛顿第二定律可得:mgsinθ —F = ma
可得:
(3)线圈从初始位置到全部穿过磁场区域减少的重力势能是3mgbsinθ,根据能量守恒有:
考点:法拉第电磁感应定律;牛顿定律及机械能守恒定律。

练习册系列答案
相关题目
为了研究超重与失重现象,某同学把一体重计放在电梯的地板上,并将一物体放在体重计上随电梯运动并观察体重计示数的变化情况.下表记录了几个特定时刻体重计的示数(表内时间不表示先后顺序)
| 时间 | t0 | t1 | t2 | t3 |
| 体重计示数(kg) | 45.0 | 50.0 | 40.0 | 45.0 |
A.t1和t2时刻电梯的加速度方向一定相反
B.t1和t2时刻物体的质量并没有发生变化,但所受重力发生了变化
C.t1和t2时刻电梯运动的加速度大小相等,运动方向一定相反
D.t3时刻电梯处于静止状态
如右图所示,一平行板电容器,右极板接电源正极,板长为2d,板间距离为d。一带电量为q、质量为m的负离子(重力不计)以速度v0贴近左极板沿极板方向射入,恰从右极板下边缘射出。在右极板右侧空间存在垂直纸面方向的匀强磁场(未标出)。要使该负离子在磁场中运动后,又恰能直接从右极板上边缘进入电场,则
| A.磁场方向垂直纸面向里 |
| B.磁场方向垂直纸面向外 |
C.磁感应强度大小为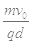 |
D.在磁场中运动时间为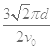 |
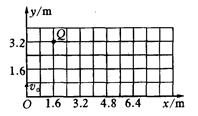
如图所示,MN是纸面内的一条直线,其所在空间充满与纸面平行的匀强电场或与纸面垂直的匀强磁场(场区都足够大),现有一重力不计的带电粒子从MN上的O点以水平初速度v0射入场区,下列有关判断正确的是( )
| A.如果粒子回到MN上时速度增大,则该空间存在的一定是电场 |
| B.如果粒子回到MN上时速度大小不变,则该空间只存在磁场 |
| C.若只改变粒子的速度大小,发现粒子再回到MN上时与其所成夹角不变,则该空间存在的一定是磁场 |
| D.若只改变粒子的速度大小,发现粒子再回到MN所用的时间不变,则该空间存在的一定是磁场 |

 .初速度为零的电子经电压为U1的电场加速后从两平行板间的中央处垂直进入偏转电场,设电子质量为m、电荷量为e .求:
.初速度为零的电子经电压为U1的电场加速后从两平行板间的中央处垂直进入偏转电场,设电子质量为m、电荷量为e .求: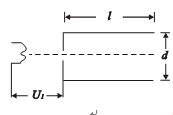
 ,0)由静止释放后沿直线PQ运动。当微粒到达点Q(0,-l)的瞬间,撤去电场同时加上一个垂直于纸面向外的匀强磁场(图中未画出),磁感应强度的大小
,0)由静止释放后沿直线PQ运动。当微粒到达点Q(0,-l)的瞬间,撤去电场同时加上一个垂直于纸面向外的匀强磁场(图中未画出),磁感应强度的大小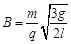 ,该磁场有理想的下边界,其他方向范围无限大。已知重力加速度为g。求:
,该磁场有理想的下边界,其他方向范围无限大。已知重力加速度为g。求:
 平面内的第一象限内存在沿
平面内的第一象限内存在沿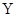 轴正方向的匀强电场,在第四象限存在有界的磁场,磁感应强度
轴正方向的匀强电场,在第四象限存在有界的磁场,磁感应强度 ,有一质量为
,有一质量为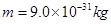 ,电量为
,电量为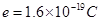 的电子以
的电子以 的速度从
的速度从 点(0,
点(0, cm)沿
cm)沿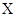 轴正方向射入第一象限,偏转后从
轴正方向射入第一象限,偏转后从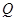 点射入第四象限,方向与
点射入第四象限,方向与 角,在磁场中偏转后又回到
角,在磁场中偏转后又回到
 的下方有磁场,如图中所示,求
的下方有磁场,如图中所示,求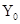 的坐标.
的坐标.