题目内容
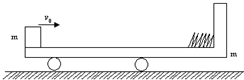
有一质量为M、长度为l的矩形绝缘板放在光滑的水平面上,另一质量为m、带电量的绝对值为q的物块(视为质点),以初速度v0从绝缘板的上表面的左端沿水平方向滑入,绝缘板周围空间是范围足够大的匀强电场区域,其场强大小E=
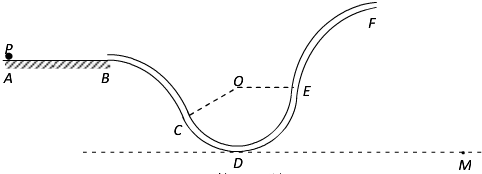
,方向竖直向下,如图所示.已知物块与绝缘板间的动摩擦因数恒定,物块运动到绝缘板的右端时恰好相对于绝缘板静止;若将匀强电场的方向改变为竖直向上,场强大小不变,且物块仍以原初速度从绝缘板左端的上表面滑入,结果两者相对静止时,物块未到达绝缘板的右端.求:
(1)场强方向竖直向下时,物场在绝缘板上滑动的过程中,系统产生的热量;
(2)场强方向竖直向下时与竖直向上时,物块受到的支持力之比;
(3)场强方向竖直向上时,物块相对于绝缘板滑行的距离.

| 3mg | 5q |
(1)场强方向竖直向下时,物场在绝缘板上滑动的过程中,系统产生的热量;
(2)场强方向竖直向下时与竖直向上时,物块受到的支持力之比;
(3)场强方向竖直向上时,物块相对于绝缘板滑行的距离.

分析:(1)滑块与矩形绝缘板系统受外力的矢量和为零,系统动量守恒,根据动量守恒定律可求解末速度;
对两次相对滑动过程根据功能关系列式求解即可;
(2)电场反向后,电场力也反向,由于第一次滑到矩形绝缘板右边缘,故第二次一定不到右边缘,故可以判断出两次的电场力方向,进一步判断两次的物块受到的支持力情况;
(3)根据功能关系列式判断场强方向竖直向上时,物块相对于绝缘板滑行的距离.
对两次相对滑动过程根据功能关系列式求解即可;
(2)电场反向后,电场力也反向,由于第一次滑到矩形绝缘板右边缘,故第二次一定不到右边缘,故可以判断出两次的电场力方向,进一步判断两次的物块受到的支持力情况;
(3)根据功能关系列式判断场强方向竖直向上时,物块相对于绝缘板滑行的距离.
解答:解:(1)场强方向竖直向下时,由系统动量守恒,有:
mv0=(m+M)v ①
由能量守恒,有:
Q1=Ff1s1=
m
-
(m+M)v2 ②
其中Q表示产生热量,Ff表示m与M间的摩擦力,s表示m与M相对位移,v表示A、B共同速度;
由①②式得:Q1=
③
同理,场强方向竖直向上时,动量仍守恒,可推出:
Q2=Q1=Ff2s2=
m
-
(m+M)v2=
④
∴Ff1s1=Ff2s2 ⑤
依题意:s1>s2,故Ff1>Ff2
而Ff=μFN ⑥
∴FN2>FN1
说明第一次电场力方向竖直向上,第二次电场力方向竖直向下(可判断物块带负电).
(2)∵FN1=mg-qE ⑦
FN2=mg+qE ⑧
由已知E=
,得
=
⑨
(3)由⑤⑥⑨得:s2=
s1=
l ⑩
答:(1)场强方向竖直向下时,物场在绝缘板上滑动的过程中,系统产生的热量为
;
(2)场强方向竖直向下时与竖直向上时,物块受到的支持力之比为1:4;
(3)场强方向竖直向上时,物块相对于绝缘板滑行的距离为
l.
mv0=(m+M)v ①
由能量守恒,有:
Q1=Ff1s1=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
其中Q表示产生热量,Ff表示m与M间的摩擦力,s表示m与M相对位移,v表示A、B共同速度;
由①②式得:Q1=
mM
| ||
| 2(m+M) |
同理,场强方向竖直向上时,动量仍守恒,可推出:
Q2=Q1=Ff2s2=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
mM
| ||
| 2(m+M) |
∴Ff1s1=Ff2s2 ⑤
依题意:s1>s2,故Ff1>Ff2
而Ff=μFN ⑥
∴FN2>FN1
说明第一次电场力方向竖直向上,第二次电场力方向竖直向下(可判断物块带负电).
(2)∵FN1=mg-qE ⑦
FN2=mg+qE ⑧
由已知E=
| 3mg |
| 5q |
| FN1 |
| FN2 |
| 1 |
| 4 |
(3)由⑤⑥⑨得:s2=
| 1 |
| 4 |
| 1 |
| 4 |
答:(1)场强方向竖直向下时,物场在绝缘板上滑动的过程中,系统产生的热量为
mM
| ||
| 2(m+M) |
(2)场强方向竖直向下时与竖直向上时,物块受到的支持力之比为1:4;
(3)场强方向竖直向上时,物块相对于绝缘板滑行的距离为
| 1 |
| 4 |
点评:本题关键根据动量守恒定律和功能关系列式后联立讨论,注意系统产生的热量是一定的,不难.

练习册系列答案
相关题目

 (1)2011年3月11日,日本东海岸发生9.0级地震,地震引发的海啸摧毁了日本福岛第一核电站的冷却系统,最终导致福岛第一核电站的6座核反应堆不同程度损坏,向空气中泄漏大量碘131和铯137等放射性物质,这些放射性物质随大气环流飘散到许多国家.4月4日,日本开始向太平洋排放大量带有放射性物质的废水,引起周边国家的指责.下列说法中正确的是:
(1)2011年3月11日,日本东海岸发生9.0级地震,地震引发的海啸摧毁了日本福岛第一核电站的冷却系统,最终导致福岛第一核电站的6座核反应堆不同程度损坏,向空气中泄漏大量碘131和铯137等放射性物质,这些放射性物质随大气环流飘散到许多国家.4月4日,日本开始向太平洋排放大量带有放射性物质的废水,引起周边国家的指责.下列说法中正确的是: