题目内容
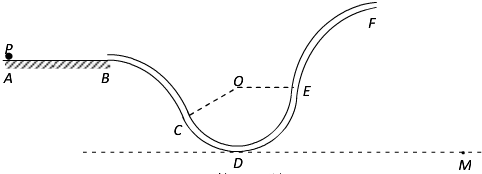
有一质量为m=0.2kg的小球,从水平轨道上的A点出发,经过一段横截面是圆形、内部光滑的固定管道后离开管道(小球半径略小于管道内径),管道由呈抛物线状的BC段、呈圆形的CDE和呈1/4圆形的EF段组成,C点、E点为连接点,E点与圆心O在同一水平线上,CO与水平方向夹角为30°,BC段的高度为h1=0.2m,CDE和EF段的半径均为R=0.3m,如图所示.小球与水平轨道间的动摩擦因数μ=0.2,AB段长度为l=0.5m,小球半径和管道的内径均远小于上述高度或半径,管壁厚度不计,所有管道与水平轨道在同一竖直面内,重力加速度g=10m/s2.
(1)若要使小球恰能从管道的F端离开,求小球从A点出发的最小速度;
(2)若小球以最小速度的2倍从A点出发,求小球经过C点的速度和经过最低点D点时小球对管道的压力;
(3)若要使小球落到离F端水平距离为0.5m的M点,求小球从A点出发的速度为多大?
(1)若要使小球恰能从管道的F端离开,求小球从A点出发的最小速度;
(2)若小球以最小速度的2倍从A点出发,求小球经过C点的速度和经过最低点D点时小球对管道的压力;
(3)若要使小球落到离F端水平距离为0.5m的M点,求小球从A点出发的速度为多大?

分析:(1)小球恰能从管道的F端离开,只要小球在管口F端时的速度为零即可,贵A-F过程,根据动能定理可求解
(2)分别对A-C过程和A-D过程应用动能定理可求出C点和D点的速度,根据向心力公式可求得小球对轨道的压力
(3)由平抛运动规律可求得小球在F点 速度,对A-F过程,根据动能定理可求解
(2)分别对A-C过程和A-D过程应用动能定理可求出C点和D点的速度,根据向心力公式可求得小球对轨道的压力
(3)由平抛运动规律可求得小球在F点 速度,对A-F过程,根据动能定理可求解
解答:解:(1)由于要求小球恰能从管道的F端离开,只要小球在管口F端时的速度为零即可,设小球从A点出发的最小速度为v1.
对小球在A-F过程中,由动能定理得:-μmgxAB-mg(R+Rsin30°-h1)=0-
m
解得:v1=
m/s
(2)当小球以最小速度的2倍(2
m/s)从A点出发时,设小球经过C点和D点的速度分别为v2、v3.
对小球在A-C过程中,由动能定理得:-μmgxAB+mgh1=
m
-
m(2v1)2
解得:v2=
m/s
对小球在A-D过程中,由动能定理得:-μmgxAB+mg(h1+R-Rsin30°)=
m
-
m(2v1)2
又:小球在D点受到重力(mg)和轨道的弹力(FN)作用,这两个力提供小球做圆周运动向心力.
由向心力公式得:FN-mg=m
由上述两式解得:FN=13N
所以小球对轨道的压力大小为13N,方向竖直向下
(3)要使小球落到M点,设小球从A点出发的速度为v4,当其到在F点时的速度为v5.
由平抛运动可知:x=v5t
2R=
gt2
又小球在A-F过程中,由动能定理得:-μmgxAB-mg(R+Rsin30°-h1)=
m
-
m
由上述三式得:v4=
m/s
答:(1)若要使小球恰能从管道的F端离开,小球从A点出发的最小速度为
m/s;
(2)若小球以最小速度的2倍从A点出发,小球经过C点的速度为
m/s
经过最低点D点时小球对管道的压力为13N;
(3)若要使小球落到离F端水平距离为0.5m的M点,小球从A点出发的速度为
m/s
对小球在A-F过程中,由动能定理得:-μmgxAB-mg(R+Rsin30°-h1)=0-
| 1 |
| 2 |
| v | 2 1 |
解得:v1=
| 7 |
(2)当小球以最小速度的2倍(2
| 7 |
对小球在A-C过程中,由动能定理得:-μmgxAB+mgh1=
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
解得:v2=
| ||
| 2 |
对小球在A-D过程中,由动能定理得:-μmgxAB+mg(h1+R-Rsin30°)=
| 1 |
| 2 |
| v | 2 3 |
| 1 |
| 2 |
又:小球在D点受到重力(mg)和轨道的弹力(FN)作用,这两个力提供小球做圆周运动向心力.
由向心力公式得:FN-mg=m
| ||
| R |
由上述两式解得:FN=13N
所以小球对轨道的压力大小为13N,方向竖直向下
(3)要使小球落到M点,设小球从A点出发的速度为v4,当其到在F点时的速度为v5.
由平抛运动可知:x=v5t
2R=
| 1 |
| 2 |
又小球在A-F过程中,由动能定理得:-μmgxAB-mg(R+Rsin30°-h1)=
| 1 |
| 2 |
| v | 2 5 |
| 1 |
| 2 |
| v | 2 4 |
由上述三式得:v4=
| ||
| 6 |
答:(1)若要使小球恰能从管道的F端离开,小球从A点出发的最小速度为
| 7 |
(2)若小球以最小速度的2倍从A点出发,小球经过C点的速度为
| ||
| 2 |
经过最低点D点时小球对管道的压力为13N;
(3)若要使小球落到离F端水平距离为0.5m的M点,小球从A点出发的速度为
| ||
| 6 |
点评:本题主要考查动能定理的应用,根据题目分段列式求解,能力要求较高,题目有一定的难度.

练习册系列答案
相关题目