题目内容
【题目】如图所示，停放在水平冰面上的冰车由质量为M，倾角为θ的斜面体改装而成，在斜面上轻放一质量为m的物块，不计物块与斜面、冰车与冰面之间的摩擦。
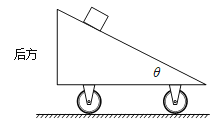
(1)释放物块后，在物块沿斜面向下运动的同时，冰车也在水平冰面上运动。请画出冰车受力的示意图，并根据示意图说明冰车由静止变为运动的原因（作图时冰车可视为质点）。
(2)若冰面上的人在车后方用水平方向的力推车，请分析下列两种可能情况：
a. 当力的大小为F1时，物块在斜面上滑动的同时冰车在冰面上保持静止，求F1和物块加速度的大小a1；
b. 当力的大小为F2时，物块和斜面保持相对静止一起加速运动，求F2和物块加速度的大小a2。
(3)第(1)问和第(2)问a所述的两种情况下，小物块对斜面压力的大小不同，分别记为FN1和 FN2，请对FN1和 FN2的大小关系作出猜想，并说明做出该种猜想的理由。
【答案】(1)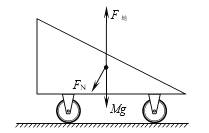 
将FN沿水平方向和竖直方向正交分解，可知竖直方向合力为零，水平方向合力不为零，因此冰车在水平方向合力作用下由静止变为运动，且在物块滑离斜面前沿水平冰面做加速运动。
(2)a：a1=gsinθ； F1= mgcosθsinθ b. a2= gtanθ； F2=（m+M）gtanθ
(3)正确的猜想：FN1 <FN2
【解析】
（1）对冰车受力分析，冰车水平方向合力不为零，所以沿水平方向做加速运动；
（2）冰车静止，水平方向合力为零，根据平衡条件列方程可求F1。分析物块的受力，根据牛顿第二定律可求小物块的加速度；当冰车与小物块相对静止时，隔离小物块可求加速度，再根据整体运用牛顿第二定律，可求F2的大小；
（3）物块加速度不沿斜面方向，将加速度a沿垂直斜面和沿斜面两方向正交分解，根据牛顿第二定律可分析重力垂直斜面的分力与支持力的关系，即可比较两种情况支持力的大小。
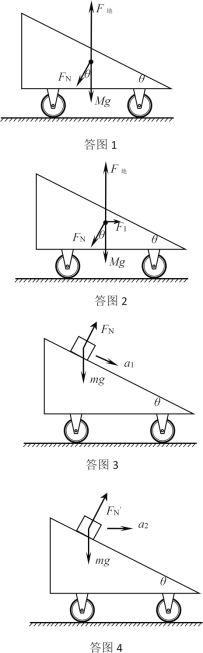
（1）冰车的受力示意图如答图1所示；
将FN沿水平方向和竖直方向正交分解，可知竖直方向合力为零，水平方向合力不为零，因此冰车在水平方向合力作用下由静止变为运动，且在物块滑离斜面前沿水平冰面做加速运动。
（2）a. 冰面上的人在车后方推车时车的受力情况如答图2所示，物块的受力情况如答图3所示
由于冰车保持静止，水平方向受力平衡，有：F1=FNsinθ
对物块应用牛顿第二定律，有：FN=mgcosθ；mgsinθ=ma1
解得：a1=gsinθ； F1= mgcosθsinθ
b. 当物块和斜面保持相对静止一起加速运动时，它们的加速度a2必然沿水平方向，物块的受力示意图如答图4所示
对物块应用牛顿第二定律，有：mgtanθ= ma2
对物块和冰车的整体应用牛顿第二定律，有：F2=（m+M）a2
解得：a2= gtanθ； F2=（m+M）gtanθ
（3）正确的猜想：FN1 <FN2；
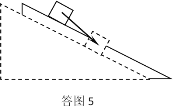
理由：第（1）问所述情况中物块沿斜面下滑的同时，斜面体沿水平冰面后退，在一小段时间内物块发生的位移x（以地面为参考系）如答图5所示，物块加速度a的方向与位移x的方向一致。将加速度a沿垂直斜面和沿斜面两方向正交分解，可知，a有垂直斜面向下的分量，结合答图3中的受力分析，可知FN1<mgcosθ；而第（2）问a所述情况中FN2=mgcosθ，因此，FN1 <FN2。
