题目内容
17.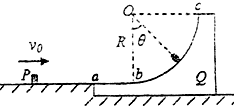 Q为一个原来静止在光滑水平面上的物体,质量为M,它带有一个凹形的不光滑轨道,轨道的ab段是水平的直线,bc段是位于竖直平面内半径为R的$\frac{1}{4}$圆弧,ab恰是圆弧bc的切线,P是另一个可看作质点的小物体,质量为m,它与轨道间的动摩擦因数为μ,物体P以沿水平方向的初速度v0冲上Q的轨道,已知它恰好能到达轨道顶端c点,后又沿轨道滑下,并最终在a点停止滑动,然后与Q一起在水平面上运动.
Q为一个原来静止在光滑水平面上的物体,质量为M,它带有一个凹形的不光滑轨道,轨道的ab段是水平的直线,bc段是位于竖直平面内半径为R的$\frac{1}{4}$圆弧,ab恰是圆弧bc的切线,P是另一个可看作质点的小物体,质量为m,它与轨道间的动摩擦因数为μ,物体P以沿水平方向的初速度v0冲上Q的轨道,已知它恰好能到达轨道顶端c点,后又沿轨道滑下,并最终在a点停止滑动,然后与Q一起在水平面上运动.①求P从a点滑动到c点的过程中,系统产生的热量;
②经过轨道的哪个位置时(要求用图中的角θ表示),Q的速度达到最大?
分析 (1)当P到达C点,P、Q具有共同的水平速度v,根据系统水平方向动量守恒,求出共同速度,再根据系统的能量守恒列方程,求解热量Q.
(2)分析P从C滑到b的过程中Q的受力,作出力图,只有Q在水平方向受力平衡时速度才最大,即可根据力图求解.
解答 解:(1)当P到达C点,P、Q具有共同的水平速度v,则系统水平方向动量守恒有:
mv0=(m+M)v
根据系统的能量守恒有:$\frac{1}{2}$mv02=$\frac{1}{2}$(m+M)v2+mgR+Q
Q=$\frac{Mm{v}_{0}^{2}}{2(m+M)}$-mgR
(2)分析P从C滑到b的过程中Q的受力.如图所示,只有Q在水平方向受力平衡时速度才最大,此时有
fcosθ=Nsin θ
θ
而 f=μN
故tgθ=μ
即P所在位置的半径与竖直方向的夹角为θ=arctgμ
答:
(1)P从a点滑动到C点过程中,系统产生的热量为$\frac{Mm{v}_{0}^{2}}{2(m+M)}$-mgR;
(2)P所在位置的半径与竖直方向的夹角为θ=arctgμ时,Q的速度达到最大
点评 本题是系统水平方向动量守恒和能量守恒的综合题,关键要根据Q的受力情况,判断出其在水平方向的合力为零时速度最大这个临界条件.

练习册系列答案
相关题目
7. 如图所示,三条虚线表示某电场中的三个等势面,其电势分别为φ1=10V,φ2=20V,φ3=30V.图中实线AB是一个带电粒子只受电场力作用下运动的轨迹则( )
如图所示,三条虚线表示某电场中的三个等势面,其电势分别为φ1=10V,φ2=20V,φ3=30V.图中实线AB是一个带电粒子只受电场力作用下运动的轨迹则( )
 如图所示,三条虚线表示某电场中的三个等势面,其电势分别为φ1=10V,φ2=20V,φ3=30V.图中实线AB是一个带电粒子只受电场力作用下运动的轨迹则( )
如图所示,三条虚线表示某电场中的三个等势面,其电势分别为φ1=10V,φ2=20V,φ3=30V.图中实线AB是一个带电粒子只受电场力作用下运动的轨迹则( )| A. | 粒子带负电,且一定是从A运动到B | |
| B. | 粒子在A点的速度大于在B点的速度 | |
| C. | 粒子在A点的加速度大于在B点的加速度 | |
| D. | 粒子在A点的电势能大于在B点的电势能 |
8. 三个点电荷A,B,C固定在正方形的三个顶点,如图所示,点电荷A带电量为+2q,B,C带电量均为-q,下列判断正确的是( )
三个点电荷A,B,C固定在正方形的三个顶点,如图所示,点电荷A带电量为+2q,B,C带电量均为-q,下列判断正确的是( )
 三个点电荷A,B,C固定在正方形的三个顶点,如图所示,点电荷A带电量为+2q,B,C带电量均为-q,下列判断正确的是( )
三个点电荷A,B,C固定在正方形的三个顶点,如图所示,点电荷A带电量为+2q,B,C带电量均为-q,下列判断正确的是( )| A. | 将点电荷A移动到无穷远,电场力对其做负功 | |
| B. | 将点电荷B移动到无穷远,电场力对其做正功 | |
| C. | 在D点放置合适的点电荷,释放点电荷A,A可能处于状态静止 | |
| D. | 在D点放置合适的点电荷,释放点电荷B.B可能处于静止状态 |
2.关于静电场,下列说法正确的是( )
| A. | 在电场中,电势越高的地方,负电荷在该点具有的电势能越小 | |
| B. | 把负电荷从A点移到B点电场力做正功,则有UAB>0 | |
| C. | 在电场中电场强度大的地方,电势一定高 | |
| D. | 任一点的电场强度总是指向该点电势降落最快的方向 |
9.下列关于分子运动和热现象的说法正确的是( )
| A. | 一定量100℃的水变成100℃的水蒸气,其分子之间的势能增加 | |
| B. | 气体如果失去了容器的约束就会散开,这是因为气体分子之间存在势能的缘故 | |
| C. | 如果气体温度升高,那么所有分子的速率都增加 | |
| D. | 如果气体分子总数不变,而气体温度升高,气体分子的平均动能增大,因此压强必然增大 | |
| E. | 对于一定质量的气体,如果压强不变,体积增大,那么它一定从外界吸热 | |
| F. | 一定量气体的内能不等于其所有分子热运动动能和分子之间势能的总和 |
7.如图所示是一交变电流的i-t图象,则该交流电电流的有效值为( )


| A. | 4A | B. | 3 A | C. | 2$\sqrt{3}$ A | D. | 2$\sqrt{2}$A |
