Question

【题目】有两列简谐横波a、b在同一介质中分别沿x轴正、负方向传播，振幅均为0.1 m，速度均为v=5 m/s，在t=0时，两列波的波峰正好在x=2.5m处重合，如图所示．求：

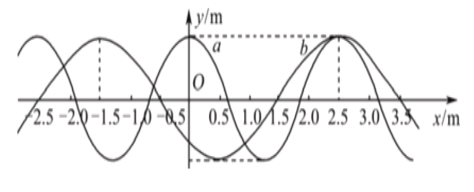
（i）t=0时，两列波的波峰重合处的位置；

（ii）从t=0开始计时，至少经过多长时间介质中出现位移为-0.2 m的质点．

Answer 1

【答案】（i）x=（2.5±20n）m,（n=0，2，3…） （ii）0.025s

【解析】

（i）从图中可以看出两列波的波长分别为=2.5 m，=4m；两列波波长的最小公倍数为s=20 m，t=0时两列波的波峰重合处的位置为：

x=（2. 5±20n）m（n=0，2，3…）

（ii）两列波的波谷对应的坐标之差：

化简得：

（m1，m2为整数）

则：

△xmin=0.25m

所以：

tmin==0.025 s

答：（i）t=0时，两列波的波峰重合处的位置x=（2. 5±20n）m（n=0，2，3…）；

（ii）从t=0开始计时，至少经过0.025s介质中出现位移为-0.2 m的质点