题目内容
【题目】如图甲所示,一固定在地面上的足够长斜面,倾角为37°,物体A放在斜面底端挡板处,通过不可伸长的轻质绳跨过光滑轻质滑轮与物体B相连接,B的质量M=1kg,绳绷直时B离地面有一定高度。在t=0时刻,无初速度释放B,由固定在A上的速度传感器得到的数据绘出的A沿斜面向上运动的v﹣t图象如图乙所示,若B落地后不反弹,g取10m/s2,sin37°=0.6,cos37°=0.8,则( )
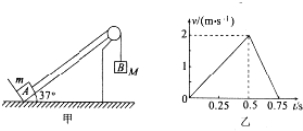
A. B下落的加速度大小a=4m/s2
B. A沿斜面向上运动的过程中,绳的拉力对A做的功W=3J
C. A的质量m=1.5Kg
D. A与斜面间的动摩擦因数μ=0.25
【答案】ABD
【解析】
AB具有相同的加速度,由图可知B的加速度为:![]() ,故A正确。设绳的拉力为T,对B由牛顿第二定律:Mg-T=Ma,解得:T=Mg-Ma=1×10-1×4=6N,AB位移相同则由图可知A上升阶段,A的位移为:x=
,故A正确。设绳的拉力为T,对B由牛顿第二定律:Mg-T=Ma,解得:T=Mg-Ma=1×10-1×4=6N,AB位移相同则由图可知A上升阶段,A的位移为:x=![]() ×2×0.5=0.5m,故绳的拉力对A做功为:W=Tx=6×0.5J=3J,故B正确。由图可知后0.25s时间A的加速度大小为:
×2×0.5=0.5m,故绳的拉力对A做功为:W=Tx=6×0.5J=3J,故B正确。由图可知后0.25s时间A的加速度大小为:![]() ,此过程A只受摩擦力和重力:μmgcosθ+mgsinθ=ma′,解得:
,此过程A只受摩擦力和重力:μmgcosθ+mgsinθ=ma′,解得:![]() ,故C错误。上升过程中,对A根据牛顿第二定律得:
,故C错误。上升过程中,对A根据牛顿第二定律得:
T-mgsinθ-μmgcosθ=ma,解得A的质量:m=0.5kg,选项C错误。

练习册系列答案
相关题目