题目内容
物理--选修3-4
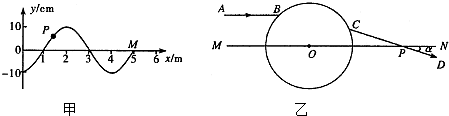
(1)如图1所示为某时刻从O点同时发出的两列简谐横波在同一介质中沿相同方向传播的波形图,P点在甲波最大位移处,Q点在乙波最大位移处,下列说法中正确的是
A.两列波传播相同距离时,乙波所用的时间比甲波的短
B.P点比Q点先回到平衡位置
C.在P质点完成20次全振动的时间内Q质点可完成30次全振动
D.甲波和乙波在空间相遇处不会产生稳定的干涉图样
(2)如图2所示,MN是一条通过透明球体球心的直线.在真空中波长为λ0=564nm的单色细光束AB平行于MN射向球体,B为入射点,若出射光线CD与MN的交点P到球心O的距离是球半径的
倍,且与MN所成的角α=30°.
(3)将光路补充完整,标明相应的入射角i和折射角r;
(4)求透明体的折射率.

(1)如图1所示为某时刻从O点同时发出的两列简谐横波在同一介质中沿相同方向传播的波形图,P点在甲波最大位移处,Q点在乙波最大位移处,下列说法中正确的是
CD
CD
:A.两列波传播相同距离时,乙波所用的时间比甲波的短
B.P点比Q点先回到平衡位置
C.在P质点完成20次全振动的时间内Q质点可完成30次全振动
D.甲波和乙波在空间相遇处不会产生稳定的干涉图样
(2)如图2所示,MN是一条通过透明球体球心的直线.在真空中波长为λ0=564nm的单色细光束AB平行于MN射向球体,B为入射点,若出射光线CD与MN的交点P到球心O的距离是球半径的
| 2 |
(3)将光路补充完整,标明相应的入射角i和折射角r;
(4)求透明体的折射率.

分析:(1)两列简谐横波在同一介质中波速相同,传播相同距离所用时间相同.Q点与P点都要经过
周期回到平衡位置.由图可两列波波长的大小,再分析周期的长短,再比较时间长短.根据频率关系研究相同时间内全振动次数关系.两列波只有频率相同时,才能产生稳定的干涉.
(2)光线沿AB直线穿过玻璃,射到圆弧面上发生折射后射到P点,作出光路图,根据数学知识求出入射角和折射角,再由折射定律求出折射率.
| 1 |
| 4 |
(2)光线沿AB直线穿过玻璃,射到圆弧面上发生折射后射到P点,作出光路图,根据数学知识求出入射角和折射角,再由折射定律求出折射率.
解答:解:(1)A、两列简谐横波在同一介质中波速相同,传播相同距离所用时间相同.故A错误.
B、由图可知,两列波波长之比λ甲:λ乙=3:2,波速相同,由波速公式v=
得到周期之比为T甲:T乙=3:2.Q点与P点都要经过
周期回到平衡位置.所以Q点比P点先回到平衡位置.故B错误.
C、两列波的频率之比为f甲:f乙=3:2,则在P质点完成20次全振动的时间内Q质点完成了30次全振动.故C正确.
D、两列波的频率不同,不能产生稳定的干涉图样.故D正确.
故选:CD
(2)连接OB、BC,在B点光线的入射角、折射角分别标为i、r,如图所示.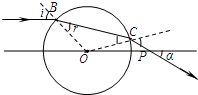
(3)在△OCP中:有
=
解得∠OCP=135°
进而可得:∠COP=15°
由折射率定义:在B点有:n=
在C点有:n=
,
又∠BCO=r
所以,i=45°
又:∠BCO=180°-i-∠COP=120°故:r=30°
因此,透明体的折射率n=
=
=
B、由图可知,两列波波长之比λ甲:λ乙=3:2,波速相同,由波速公式v=
| λ |
| T |
| 1 |
| 4 |
C、两列波的频率之比为f甲:f乙=3:2,则在P质点完成20次全振动的时间内Q质点完成了30次全振动.故C正确.
D、两列波的频率不同,不能产生稳定的干涉图样.故D正确.
故选:CD
(2)连接OB、BC,在B点光线的入射角、折射角分别标为i、r,如图所示.

(3)在△OCP中:有
| OC |
| sinα |
| OP |
| sin∠OCP |
解得∠OCP=135°
进而可得:∠COP=15°
由折射率定义:在B点有:n=
| sini |
| sinr |
在C点有:n=
| sin(180°-135°) |
| sin∠BCO |
又∠BCO=r
所以,i=45°
又:∠BCO=180°-i-∠COP=120°故:r=30°
因此,透明体的折射率n=
| sini |
| sinr |
| sin45° |
| sin30° |
| 2 |
点评:(1)本题关键要抓住波速是由介质的性质决定的,在同一介质中传播的同类波速度相同.常规题.
(2)本题考查光的折射.关键是作出光路图,根据几何知识求出入射角与折射角.
(2)本题考查光的折射.关键是作出光路图,根据几何知识求出入射角与折射角.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 【物理-选修3-4】
【物理-选修3-4】

 【物理--选修3-4】
【物理--选修3-4】