题目内容
【题目】1930年,Earnest O. Lawrence提出了回旋加速器的理论,他设想用磁场使带电粒子沿圆弧形轨道旋转,多次反复地通过高频加速电场,直至达到高能量。题图甲为Earnest O. Lawrence设计的回旋加速器的示意图。它由两个铝制D型金属扁盒组成,两个D形盒正中间开有一条狭缝;两个D型盒处在匀强磁场中并接有高频交变电压。图乙为俯视图,在D型盒上半面中心S处有一正离子源,它发出的正离子,经狭缝电压加速后,进入D型盒中。在磁场力的作用下运动半周,再经狭缝电压加速;为保证粒子每次经过狭缝都被加速,应设法使交变电压的周期与粒子在狭缝及磁场中运动的周期一致。如此周而复始,最后到达D型盒的边缘,获得最大速度后被束流提取装置提取出。已知正离子的电荷量为q,质量为m,加速时电极间电压大小恒为U,磁场的磁感应强度为B,D型盒的半径为R,狭缝之间的距离为d。设正离子从离子源出发时的初速度为零。
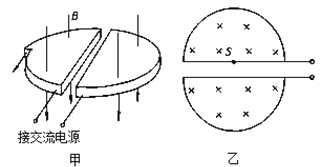
(1)试计算上述正离子从离子源出发被第一次加速后进入下半盒中运动的轨道半径;
(2)设该正离子在电场中的加速次数与回旋半周的次数相同,试推证当R>>d时,正离子在电场中加速的总时间相对于在D形盒中回旋的时间可忽略不计(正离子在电场中运动时,不考虑磁场的影响)。
(3)若此回旋加速器原来加速的是α粒子(![]() ),现改为加速氘核(
),现改为加速氘核(![]() ),要想使氘核获得与α粒子相同的动能,请你通过分析,提出一种简单可行的办法。
),要想使氘核获得与α粒子相同的动能,请你通过分析,提出一种简单可行的办法。
【答案】(1)![]() (2)见解析(3)
(2)见解析(3)![]()
【解析】
(1)设质子经过窄缝被第n次加速后速度为vn,由动能定理nqU=![]() mvn2
mvn2
第n次加速后质子在磁场中做匀速圆周运动的半径为Rn,由牛顿第二定律Bqvn=m![]()
由以上两式解得![]()
则R1=![]() ;
;
(2)在电场中加速的总时间为:![]()
在D形盒中回旋的时间为t2=![]()
故![]() 1
1
即只有当Rd时,质子在电场中加速的总时间相对于在D形盒中回旋的时间可忽略不计.
(3)若加速氘核,氘核从D盒边缘离开时的动能为Ek′则:Ek′=![]() =Ekm
=Ekm
联立解得B1=![]() B
B
即磁感应强度需增大为原来的![]() 倍;高频交流电源的周期T=
倍;高频交流电源的周期T=![]() ,由α粒子换为氘核时,交流电源的周期应为原来的
,由α粒子换为氘核时,交流电源的周期应为原来的![]() 倍.
倍.

【题目】(1)在做“探究平抛运动”的实验时,让小球多次从同一高度释放沿同一轨道运动,通过描点法画小球做平抛运动的轨迹.为了能较准确地描绘运动轨迹.下面列出了一些操作要求,将正确的选项前面的字母填在横线上________.
A.调节斜槽的末端保持水平 |
B.每次释放小球的位置必须不同 |
C.每次必须由静止释放小球 |
D.记录小球位置用的凹槽每次必须严格地等距离下降 |
E.小球运动时不应与木板上的白纸(或方格纸)相接触
F.将球的位置记录在纸上后,取下纸,用直尺将点连成折线
(2)未来在一个未知星球上用如图甲所示装置研究平抛运动的规律.悬点O正下方P点处有水平放置的炽热电热丝,当悬线摆至电热丝处时能轻易被烧断,小球由于惯性向前飞出做平抛运动.现对小球采用频闪数码照相机连续拍摄.在有坐标纸的背景屏前,拍下了小球在做平抛运动过程中的多张照片,经合成后,照片如图乙所示.a、b、c、d为连续四次拍下的小球位置,已知照相机连续拍照的时间间隔是0.10 s,照片大小如图中坐标所示,又知该照片的长度与实际背景屏的长度之比为1:4,则:

①由以上信息,可知a点________(选填“是”或“不是”)小球的抛出点;
②由以上及图信息,可以推算出该星球表面的重力加速度为________m/s2;
③由以上及图信息可以算出小球平抛的初速度是________ m/s;
④由以上及图信息可以算出小球在b点时的速度是________ m/s.